Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT GUJARATI-QUADRILATERALS-EXERCISE - 8.3
- The opposite angles of a parallelogram are (3x-2)^(@) and (x+48)^(@). ...
Text Solution
|
- Find the measure of all the angles of a parallelogram, if one angle is...
Text Solution
|
- In the adjacent figure ABCD is a parallelogram and E is the midpoint o...
Text Solution
|
- In the adjacent figure ABCD is a parallelogram P and Q are the midpoin...
Text Solution
|
- ABC is an isosceles triangle in which AB = AC. AD bisects exterior ang...
Text Solution
|
- ABCD is a parallelogram AP and CQ are perpendiculars drawn from vertic...
Text Solution
|
- In Delta^(s)ABC and, AB"||"DE, BC=EF and BC"||"EF. Vertices A, B and C...
Text Solution
|
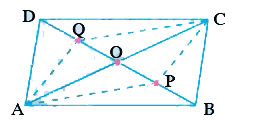
- ABCD is a parallelogram. AC and BD are the diagonals intersect at O. P...
Text Solution
|
- ABCD is a square. E, F, G and H are the mid points of AB, BC, CD and D...
Text Solution
|