Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT GUJARATI-CIRCLES-EXERCISE 12.4
- In the figure 'O' is the centre of the circle angle AOB = 100^@ f...
Text Solution
|
- In the figure angle BAD = 40^@ then find angle BCD
Text Solution
|
- In the figure , O is the centre of the circle and angle POR = 120^@ . ...
Text Solution
|
- In the figure, ‘O’ is the centre of the circle. OM = 3cm and AB = 8cm...
Text Solution
|
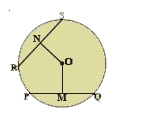
- In the figure, ‘O’ is the centre of the circle and OM, ON are the perp...
Text Solution
|
- A is the centre of the circle and ABCD is a square. If BD = 4cm then ...
Text Solution
|
- Draw a circle with any radius and then draw two chords equidistant fro...
Text Solution
|
- In the given figure ‘O’ is the centre of the circle and AB, CD are eq...
Text Solution
|