Topper's Solved these Questions
APPLICATIONS OF TRIGONOMETRY
NCERT GUJARATI|Exercise Optional Exercise (For extensive learning)|4 VideosAPPLICATIONS OF TRIGONOMETRY
NCERT GUJARATI|Exercise THINK AND DISCUSS|1 VideosAPPLICATIONS OF TRIGONOMETRY
NCERT GUJARATI|Exercise Exercise 12.1|10 VideosCOORDINATE GEOMETRY
NCERT GUJARATI|Exercise TRY THIS|10 Videos
Similar Questions
Explore conceptually related problems
NCERT GUJARATI-APPLICATIONS OF TRIGONOMETRY-Exercise 12.2
- A TV tower stands vertically on a bank of a canal. From a point on the...
Text Solution
|
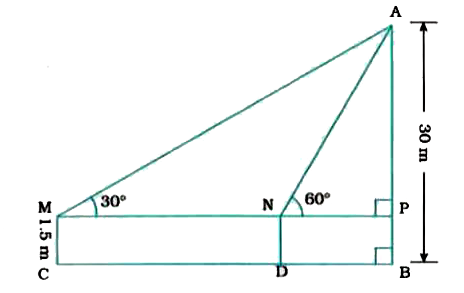
- A 1.5m tall boy is standing at some distance from a 30m tall building....
Text Solution
|
- A statue stands on the top of a 2m tall pedestal. From a point on the ...
Text Solution
|
- From the top of a building, the angle of elevation of the top of a cel...
Text Solution
|
- A wire of length 18 m had been tied with electric pole at an angle of ...
Text Solution
|
- The angle of elevation of the top of a building from the foot of the t...
Text Solution
|
- Two poles of equal heights are standing opposite to each other on eith...
Text Solution
|
- The angles of elevation of the top of a tower from two points at a dis...
Text Solution
|
- The angle of elevation of a jet plane from a point A on the ground is ...
Text Solution
|
- The angle ofelevation of the top of a tower from the foot of the build...
Text Solution
|