Text Solution
Verified by Experts
Topper's Solved these Questions
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
NCERT GUJARATI|Exercise EXERCISES|31 VideosSYSTEMS OF PARTICLES AND ROTATIONAL MOTION
NCERT GUJARATI|Exercise EXERCISES (TRUE OR FALSE)|5 VideosPHYSICAL WORLD
NCERT GUJARATI|Exercise EXERCISES|8 VideosTHERMAL PROPERTIME OF MATTER
NCERT GUJARATI|Exercise EXERCISES|31 Videos
Similar Questions
Explore conceptually related problems
NCERT GUJARATI-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-EXERCISES (TRUE OR FALSE)
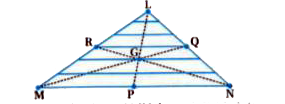
- Find the centre of mass of a triangular lamina.
Text Solution
|
- During rolling, the force of friction acts in the same direction as th...
Text Solution
|
- The instantaneous speed of the point of contact during rolling is zero...
Text Solution
|
- The instantaneous acceleration of the point of contact during rolling ...
Text Solution
|
- For perfect rolling motion, work done against friction is zero.
Text Solution
|
- A wheel moving down a perfectly frictionless inclined plane will under...
Text Solution
|