Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT GUJARATI-THERMODYNAMICS -EXERCISES
- A geyser heats water flowing at the rate of 3.0 litres per minute from...
Text Solution
|
- What amount of heat must be supplied to 2.0 xx 10^(-2) Kg of nitrogen ...
Text Solution
|
- Explain why (a) Two bodies at different temperatures T(1) and T(2) i...
Text Solution
|
- A cylinder with a movable piston contains 3 moles of hydrogen at stand...
Text Solution
|
- In changing the state of a gas adiabatically from an equilibrium state...
Text Solution
|
- Two cylinders A and B of equal capacity are connected to each other vi...
Text Solution
|
- A steam engine delivers 5.4 xx 10^8 J of work per minute and services ...
Text Solution
|
- An electric heater supplies heat to a system at a rate of 100 W. If sy...
Text Solution
|
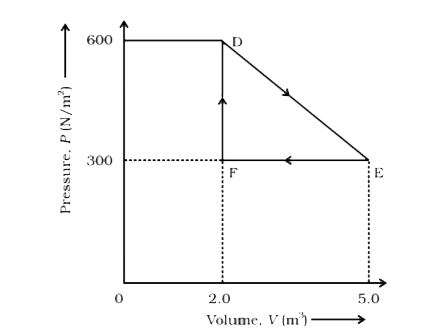
- A thermodynamic system is taken from an original state to an intermedi...
Text Solution
|
- A refrigerator is to maintain eatables kept inside at 9^(@)C. If room ...
Text Solution
|