Home
Class 12
PHYSICS
Determine the current in each brance of ...

Determine the current in each brance of the network showin in

Text Solution

Verified by Experts

Each branch of the network is assigned an unknow current to be determined by the application of Kirchhoff s rules. To reduce the number of unknowns at the unknow current in each branch. We then have three unknowns `I_(1) , I _(2) and I _(3)` which can be fond by alllying the second rule of Kirchhoff to three different closed loops. Kirchhoff.s second rule for the closed lop ADCA gives.
`10- 4 (I _(1) - I _(2)) + 2 (I _(2) + I_(3) -I _(1) - I _(1) =0`
that is, `7I _(1) - 6I_(2) - 2I_(3) =10`
For the closed loop ABCA. we get
`10-4I_(2) -2 (I _(2) + I_(3)-I_(1) =0`
that is `2I_(1) -4I_(2) -4I_(3) =-5`
Equations (`3.80a,b,c)` are three simultaneous equations in three unknowns. These can be solved by the usual method to give
` I _(1) =2.5A. I _(2) = (5)/(8) A, I _(3) =1 (7)/(8) A`
The currents in the various branches of the network are
`AB: 5/8 A, CA: 2 (1)/(2) A, DEB: 1(7)/(8) A`
`AD : 1 (7)/(8) A, CD :0A, BC: 2 (1)/(2) A`
It is easily verified that Kirchhoff.s second rule applied to the remaining closed lops does not provide any additional independent equation, that is, the above values of currents satisfy the second rule for every closed loop of the network. For example, the total voltage drop over the closed loop BADEB
`5 V + ((5)/(8) xx 4) V - ((15)/(8) xx 4) V`
equal to zero, as required by Kirchhoff s second rule.
Promotional Banner

Topper's Solved these Questions

  • CURRENT ELECTRICITY

    NCERT GUJARATI|Exercise EXERCISES|12 Videos

  • CURRENT ELECTRICITY

    NCERT GUJARATI|Exercise ADDITIONAL EXERCISES|9 Videos

  • ATOMS

    NCERT GUJARATI|Exercise ADDITIONAL EXERCISE|10 Videos

  • DUAL NATURE OF RADIATION AND MATTER

    NCERT GUJARATI|Exercise EXERCISES|41 Videos

Similar Questions

Explore conceptually related problems

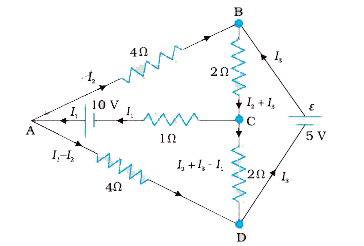
Determine the current in each branch of the given network.

Determine the equivalent resistance of networks shown in figure.

A network of four 10 µF capacitors is connected to a 500 V supply, as shown in Fig. 2.29. Determine (a) the equivalent capacitance of the network and (b) the charge on each capacitor. (Note, the charge on a capacitor is the charge on the plate with higher potential, equal and opposite to the charge on the plate with lower potential.)

(a) Given n resistores each of resistance R. how will you combine them to get the (i) maximum (ii) minimum effective resistance? (b) Given the resistances of 1 Omega, 2 Omega, 3 Omega. how will be combine them to get an equivalent resistance of (i) (11//3) Omega (ii) (11//5) Omega, (iii) 6 Omega, (iv) (6//11) Omega ? (c ) Determine the equivalent resistance of networks shown in

A bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Omega Determine the equivalent resistance of the network and the current along each edge of the cube.

Obtain the equivalent capacitance of the network in Fig. 2.33. For a 300 V supply, determine the charge and voltage across each capacitor.

Find the effective resistance between points A and B for the network shown in the figure below.

For the network of resistance shown in the figure the equivalent resistance of the network between the points A and B is 18 ohm. The value of unknown resistance R is :