Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT GUJARATI-CURRENT ELECTRICITY -EXERCISES
- The storage battery of a car has an emf of 12 V. If the internal resis...
Text Solution
|
- A bettery of emf 10 V and internal resistacne 3 Omega is connected to ...
Text Solution
|
- (a) Three resistor 1Omega ,2Omega, and 3Omega are combined in series. ...
Text Solution
|
- (a) Three resistors 2 Omega 4 Omega and 5 Omega are combined in parall...
Text Solution
|
- At room temperature (27.0^(@)C) the resistance of a heating element i...
Text Solution
|
- A negligibly small current is passed through a wire of length 15 m and...
Text Solution
|
- A silver wire has a resistance of 2.1 Omega at 27.5 ^(@)C. and a rsist...
Text Solution
|
- A heating element using nichrome connected to a 230 V supply draws an ...
Text Solution
|
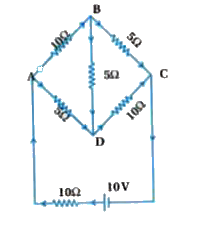
- Determine the current in each branch of the given network.
Text Solution
|
- A storage battery of emf 8.0V and internal resistance 0.5Omega is bein...
Text Solution
|
- In a potentiometer arrangement, a cell of emf 1.25V fives a balance po...
Text Solution
|
- The number density of free electrons in a copper conductor estimated i...
Text Solution
|