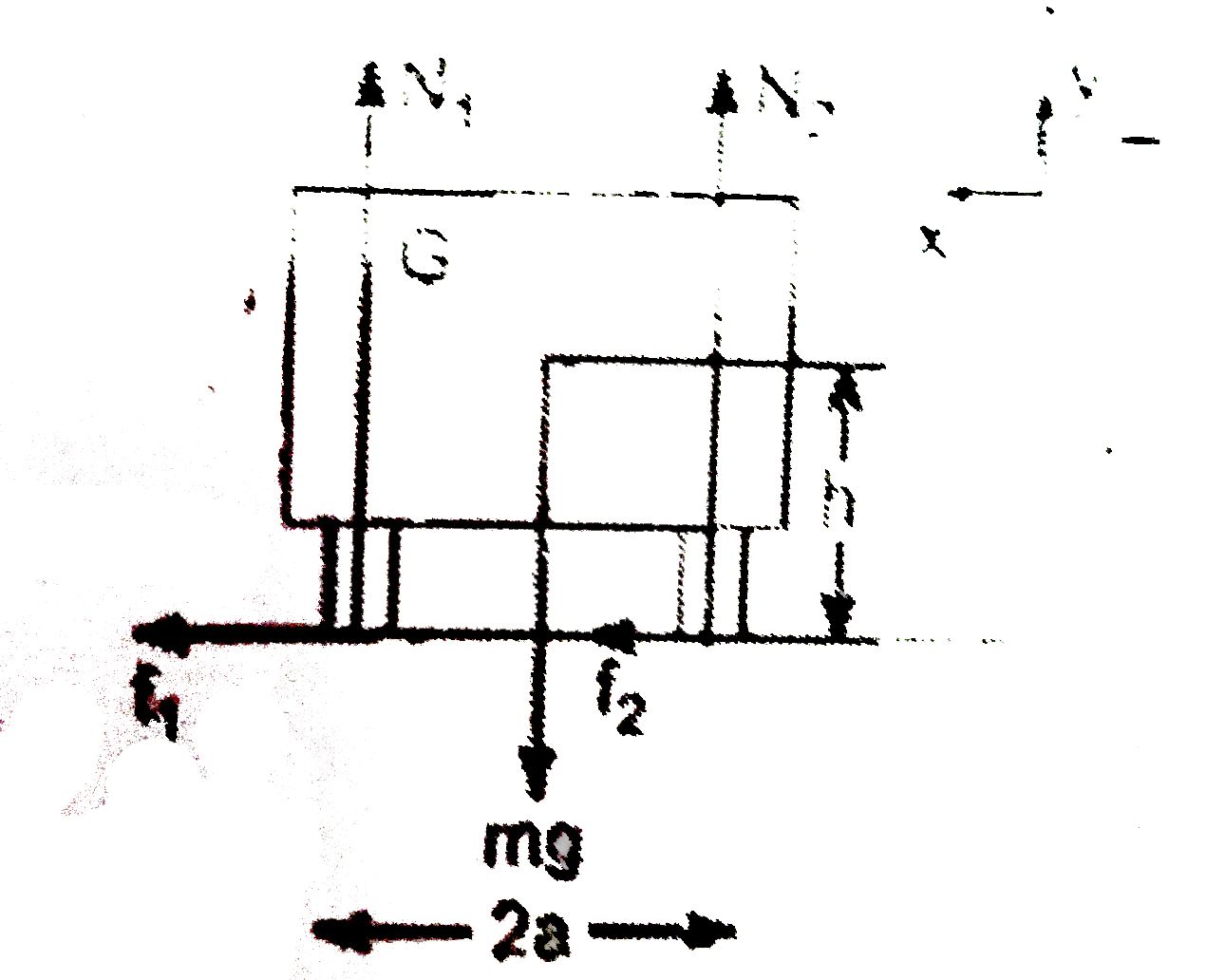Similar Questions
Explore conceptually related problems
Recommended Questions
- A car of mass m travelling at speed v moves on a horizontal track. The...
Text Solution
|
- A car moves with speed v on a horizontal circular track of radius R. A...
Text Solution
|
- A car moves with speed v on a horizontal circular track of radius R . ...
Text Solution
|
- Consider a car moving on a horizontal road, convex bridge and concave ...
Text Solution
|
- A car of mass m moves in a horizontal circular path of radius r metre....
Text Solution
|
- A car of mass m travelling at speed v moves on a horizontal track. The...
Text Solution
|
- The centre of gravity of a car is at a height h and the distance betwe...
Text Solution
|
- A car of mass m travelling at speed v moves on a horizontal track so t...
Text Solution
|
- 500 किग्रा द्रव्यमान की एक कार 50 मीटर त्रिज्या के वृत्त पर एकसमान चाल...
Text Solution
|