Similar Questions
Explore conceptually related problems
Recommended Questions
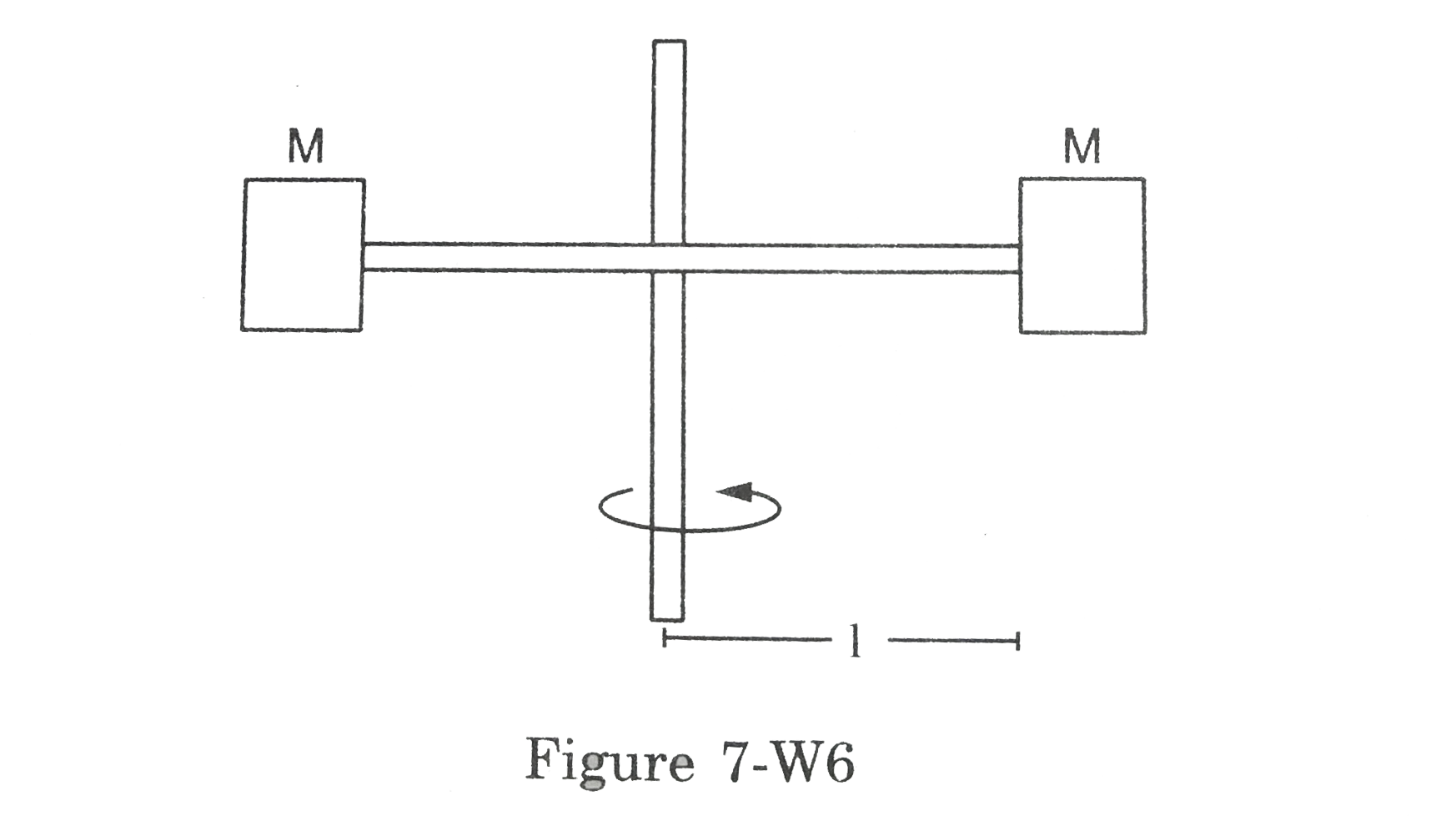
- Two blocks each of mass M are connected to the ends of a light frame a...
Text Solution
|
- Two blocks each of mass M are connected to the ends of a light frame a...
Text Solution
|
- A block of mass m is connected to a spring of spring constant k as sho...
Text Solution
|
- The rod AB oriented parallel to the x^' axis of the reference frame K^...
Text Solution
|
- Three massless rods are fixed to form a right angled triangular frame ...
Text Solution
|
- M द्रव्यमान के दो ब्लॉक एक नगण्य भार वाले फ्रेम में लगी एक नगण्य भार व...
Text Solution
|
- An equilateral triangular frame is made of three thin massless rods. T...
Text Solution
|
- As shown in the figure, a rod moves with v = 2 m/sec & rotates with om...
Text Solution
|
- Three indentical thin rods each of mass m and length L are joined toge...
Text Solution
|