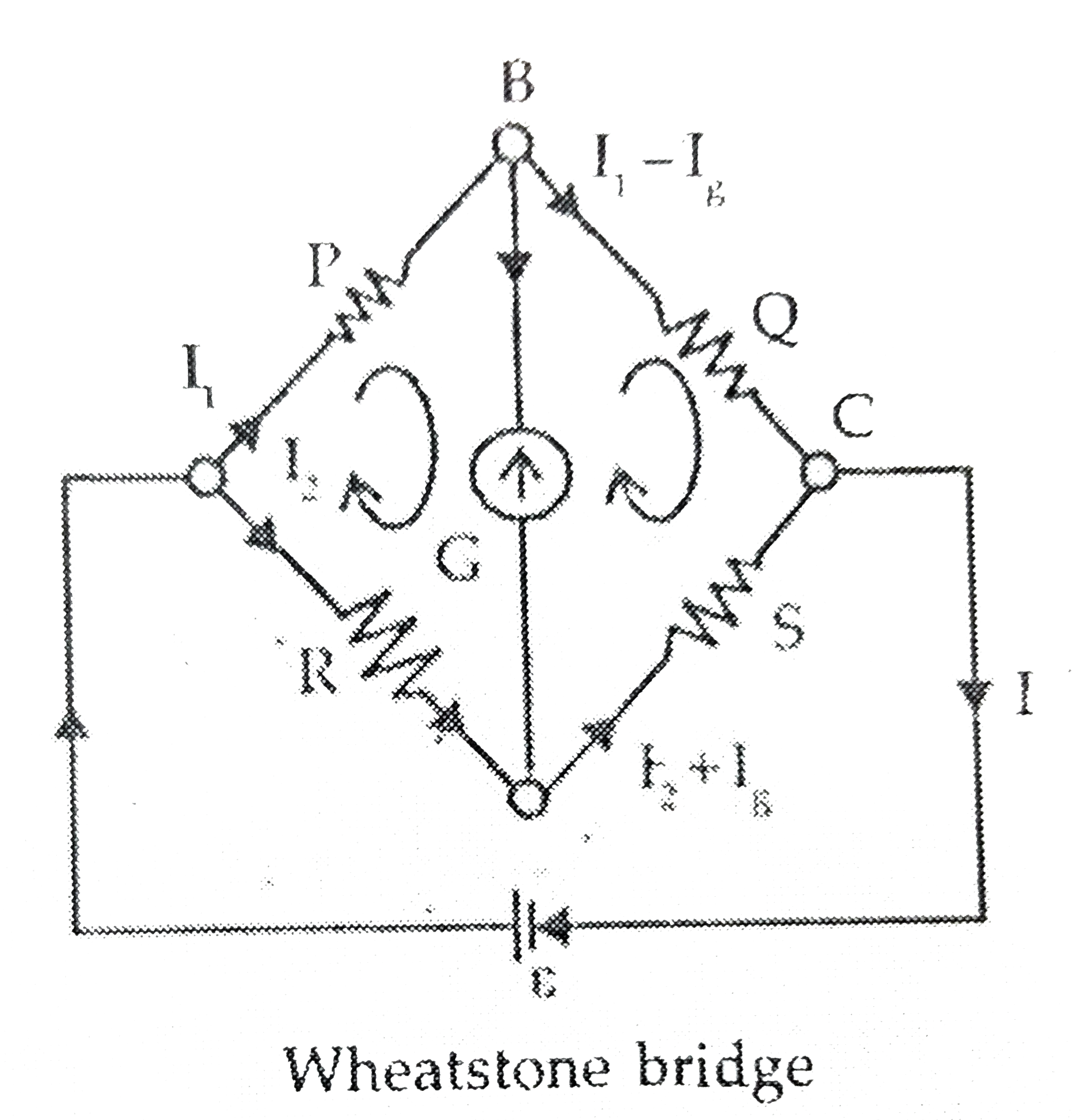
(a) Applying Kichhoff's second law of the loop ABDA, we get,
Again applying Kirchhoff's second law to the loop BCDB, we get
` (I_1-I_delta)Q-(I_2_+I_delta)S-GI_delta=0`
In the balanced condition of the bridge,`I_delta=0`. The above equations become
` I_1P-I_2R=0 or I_1P=1_2R......(i)`
and ` I_1q-i_2S=0 or I_1Q=I_2S`
On dividing equation (i) by equation (ii), we get
` (P)/(Q)=(R)/(S)`
This proves the condition for the balanced Wheatstone bridge.
(i=b) Metre bridge or slide wire bridge. it is the simplest practical application of the Wheatstone bridge that is used to measure an unknown resistance.
Principal : Its working is based on the principle of Wheatsotne bridge. When the bridge is balanced,
` (P)/(Q)=(R)/(S)`
Construction : It consists of usually one metre long magnanin wire of uniform cross - section, stretched along a matre scale ficed over a wooden board and with its two ends soldered to two L-shaped thick copper strips A and C. Between these two copper strips, another copper strip is fixed so as to provide two gaps ab and the `a_1 b _1 ` . A resistance box R.B. is connected in the gap ab and the unknown resistance S is connected in the gap ` a_1 b _1 `.A source of emf ` epsi` is connected across AC. A movable jockey and a galvanometer are connected across BD, as shown in figure.
After taking out a suitable resistance R from the resistance box, the jockey is moved along the wire AC till there is no deflection in the galvanometer. This is the balanced condition of the Wheatstone bridge. If P and Q are the resistances of the parts AB and BC of the wire, then for the balanced condition of the bridge , we have
` (P)/(Q) =(R)/(S)`.
Let total length of wire `AC=100 cm and AB= I cm`, Then`BC =(100-l) cm`. Since, the bridge wire is of uniform cross- section, therefore,
resistance of wire `prop` length of wire
` (P)/(Q)= ("resistance of AB")/("resistance of BC")`
` =(sigmal)/(singma( 100-l))=(l)/(100-l)`.
whee `sigma` is the resistance per unit length of the wire.
Hence, `(R)/(S)=(l)/(100-l)`
or ` S=(R(100-l))/(l)`