Similar Questions
Explore conceptually related problems
Recommended Questions
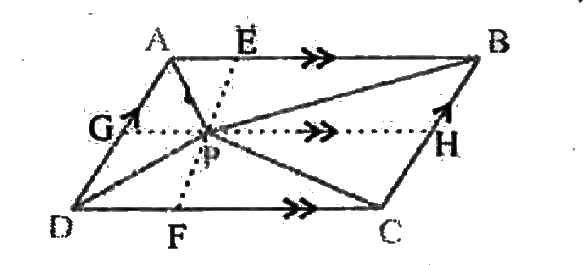
- In P is a point in the interior of a parallelogram ABCD. Show that (ii...
Text Solution
|
- In Fig. 9.16, P is a point in the interior of a parallelogram ABCD. S...
Text Solution
|
- Determine the point of symmetry of a regular hexagon. <img src="htt...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- आकृति में में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई ...
Text Solution
|
- P और Q क्रमशः समांतर चतुर्भुज ABCD की भुजाओं DC और AD पर बिन्दु है। दर...
Text Solution
|
- चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते है...
Text Solution
|
- दिए गए चित्र में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु...
Text Solution
|
- P और Q किसी समांतर चतुर्भुज ABCD की भुजाओं DC तथा AD पर स्थित दो बिंदु...
Text Solution
|