Similar Questions
Explore conceptually related problems
Recommended Questions
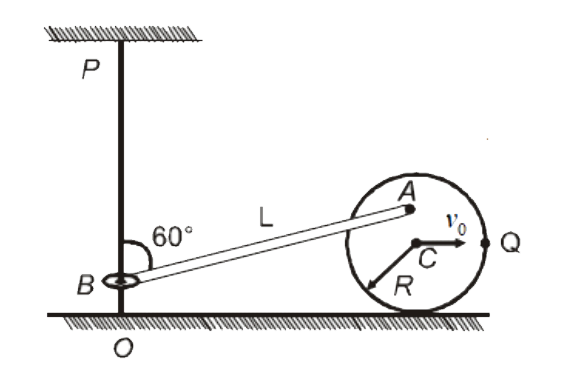
- A smooth rod OP is fixed vertically. A disc of mass m and radius R is ...
Text Solution
|
- A man of mass m stands on a horizontal platform in the shape of a disc...
Text Solution
|
- A disc of mass M and radius R can rotate freely in a vertical plane ab...
Text Solution
|
- A disc of mass M and radius R can rotate freely in a vertical plane ab...
Text Solution
|
- A disc of a mass M and radius R can rotate freely in vertical plane ab...
Text Solution
|
- A disc of radius a is ridigly attached at its circumference to a rod o...
Text Solution
|
- A uniform disc of mass M and radius R is rotating freely about its cen...
Text Solution
|
- A uniform rod of mass m and length L lies radialy on a disc rotating w...
Text Solution
|
- A smooth disc of mass M and radius (L)/(sqrt(3)) is placed at rest hor...
Text Solution
|