Similar Questions
Explore conceptually related problems
Recommended Questions
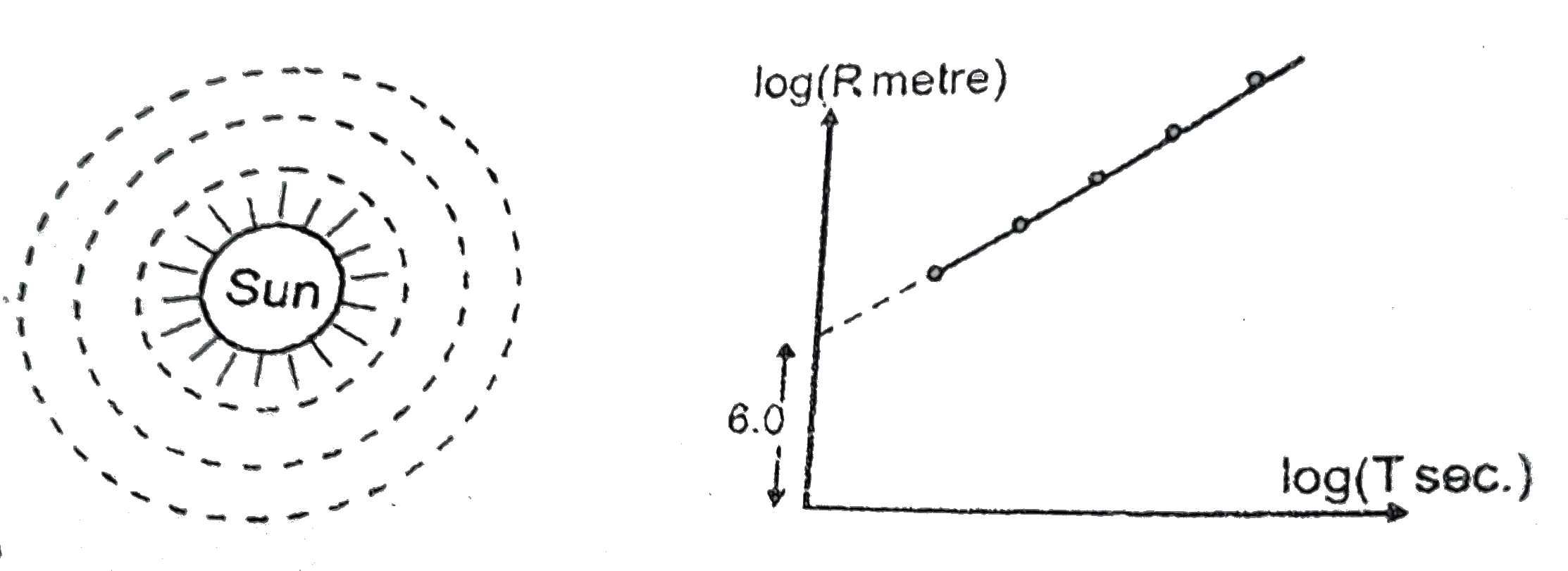
- Many planets are revolving around the fixed sun in circular orbits of ...
Text Solution
|
- If a planet of mass m is revolving around the sun in a circular orbit ...
Text Solution
|
- Many planets are revolving around the fixed sun in circular orbits of ...
Text Solution
|
- Many planets are revolving around the fixed sun in circular orbits of ...
Text Solution
|
- Many planets are revolving around the fixed sun in circular orbits of ...
Text Solution
|
- If a time period of revolution of a satellite around a planet in a cir...
Text Solution
|
- For many planets revolving around the stationary sun in circular orbit...
Text Solution
|
- If the time period of a satellite in the orbit of radius r around a pl...
Text Solution
|
- Using orbital radius r and the corresponding periodic time T of differ...
Text Solution
|
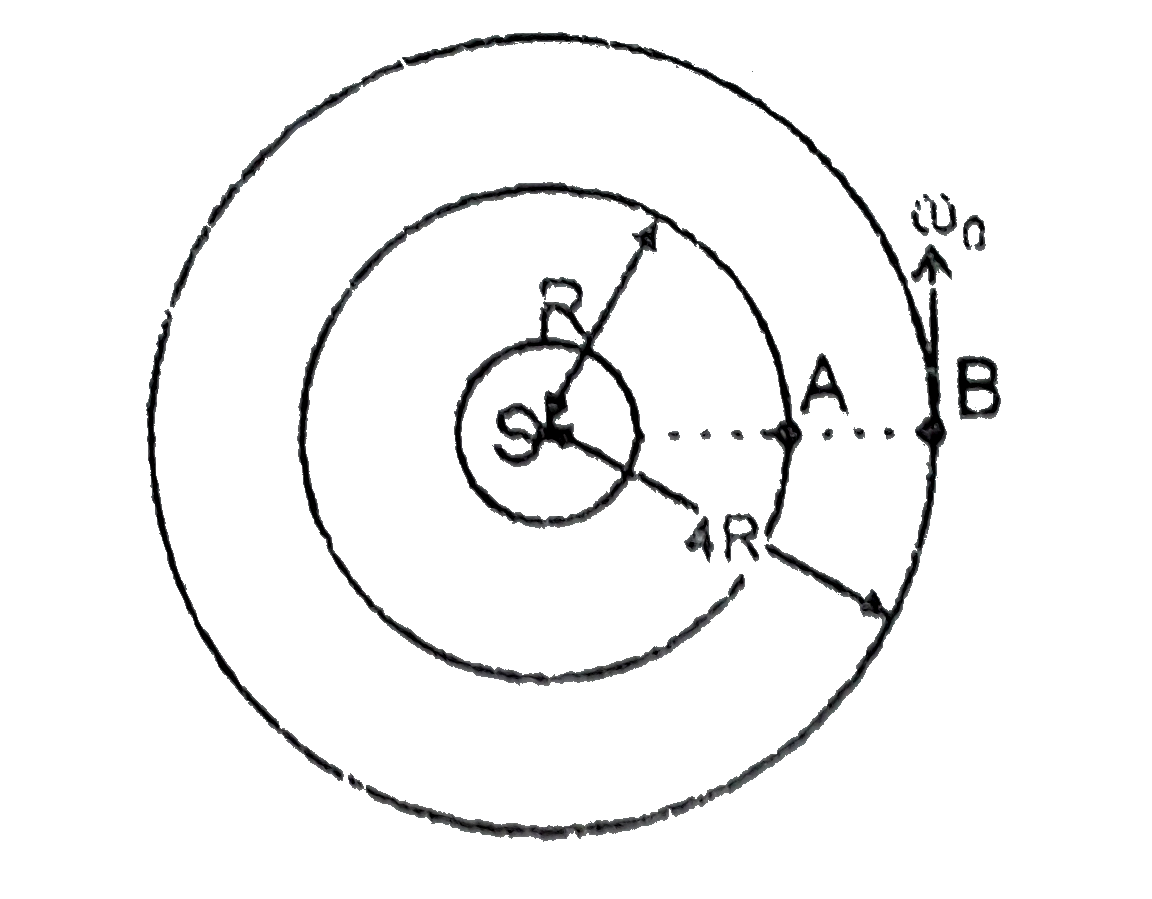 .
.