Similar Questions
Explore conceptually related problems
Recommended Questions
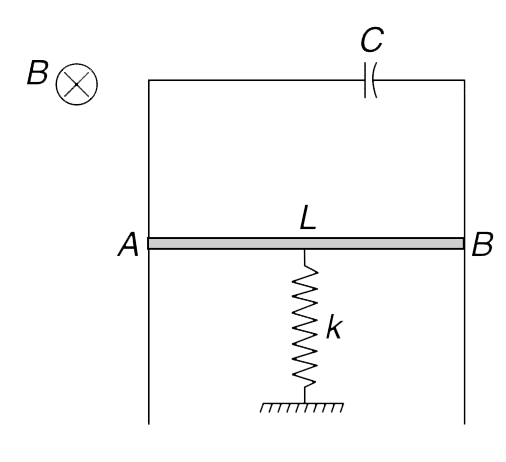
- Two metal bars are fixed vertically and are connected on top by a capa...
Text Solution
|
- Two metal bars are fixed vertically and are connected on the top by a ...
Text Solution
|
- A ring of mass m=10kg can slide through a vertical rod with friction. ...
Text Solution
|
- A conductor of length l and mass m can slide without any friction alon...
Text Solution
|
- A conductor of mass m and length l is sliding smoothly an two vertical...
Text Solution
|
- A ring of mass m can slide over a smooth vertical rod. The ring is con...
Text Solution
|
- The fig. shows an infinite tower of identical springs each having forc...
Text Solution
|
- Two blocks A and B, each of mass m, are connected by a spring of force...
Text Solution
|
- Two metal bars are fixed vertically and are connected on top by a capa...
Text Solution
|