Similar Questions
Explore conceptually related problems
Recommended Questions
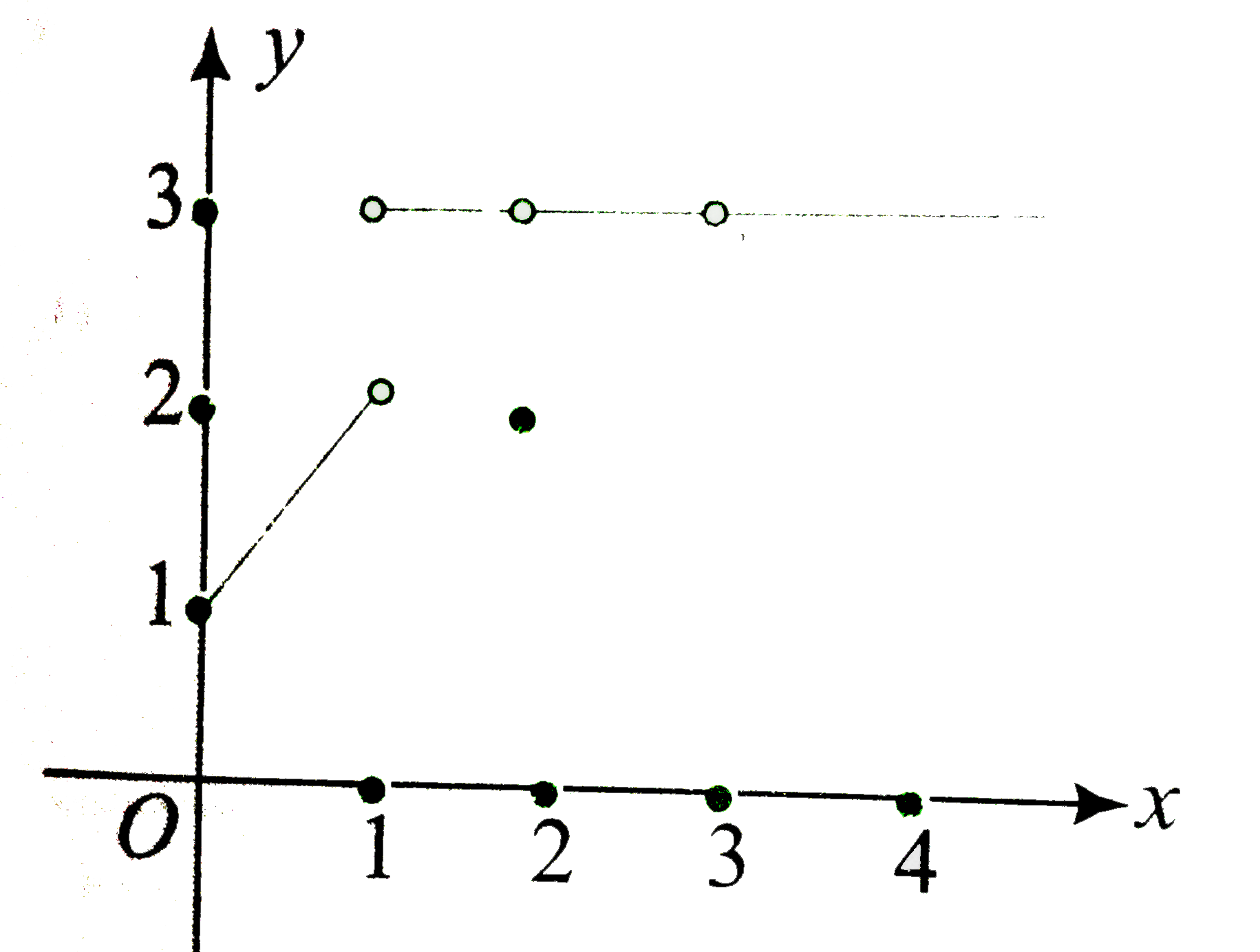
- Consider the following graph of the function y=f(x). Which of the foll...
Text Solution
|
- If ("lim")(xveca)[f(x)g(x)] exists, then both ("lim")(xveca)f(x)a n d(...
Text Solution
|
- Which of the following statements about the function y=f(x) graphed he...
Text Solution
|
- lim(x rarr c)f(x) does not exist when: (A) f(x)=[[x]]-[2x-1],c=3
Text Solution
|
- Which of the following statement(s) is (are) INCORRECT ?. (A) If lim(x...
Text Solution
|
- Consider the following graph of the function y=f(x). Which of the foll...
Text Solution
|
- If f(x)=sgn(x)" and "g(x)=x^(3),then prove that lim(xto0) f(x).g(x) ex...
Text Solution
|
- यदि f एक फलां इस प्रकार है कि f(-x)=-f(x) तथा lim(xto0)f(x) का अस्तित्...
Text Solution
|
- Statement - I: if lim(x to 0)((sinx)/(x)+f(x)) does not exist, then li...
Text Solution
|