Similar Questions
Explore conceptually related problems
Recommended Questions
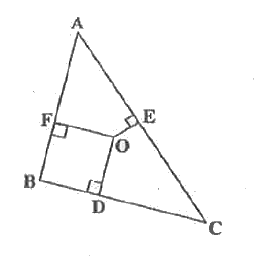
- In Fig. 2.54, o is a point in the interior of a triangle ABC,ODbotBC,...
Text Solution
|
- From a point O in the interior of a A B C , perpendiculars O...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- आकृति 6 . 54 में Delta ABC के अभ्यन्तर में स्थित कोई बिंदु O है तथा OD...
Text Solution
|
- O is a point in the interior of Delta ABC, OD bot BC, OE bot AC and O...
Text Solution
|
- triangle ABC के एक अन्तः बिंदु O से, भुजा BC,CA तथा AB पर लम्ब क्रमशः ...
Text Solution
|
- Delta ABC के अंदर बिंदु O से भुजाओ BC ,CA और AB पर क्रमश: लंब OD ,OE...
Text Solution
|
- In Fig. 2.54, o is a point in the interior of a triangle ABC,ODbotBC,...
Text Solution
|
- In Fig. 2.54, o is a point in the interior of a triangle ABC,ODbotBC,...
Text Solution
|