(a) A simple schematic diagram of Young.s double-slit experiment to produce interference pattern due to a monochromatic source of light is shown here. Let `S_(1)` and `S_(2)` be two narrow slits, a small distance .d. apart, illuminated by a monochromatic light source S of wavelength `lamda`, kept equidistant from the slits `S_(1)` and `S_(2)` and MN be a screen situated at a distance .D. from double-slit and it is parallel to double-slit. Then, we obtain alternate bright and dark fringes on the screen and the central point O of the screen is bright. Consider a point P on the screen MN, at a distance .x. from the symmetrical central point O of screen. Path difference between
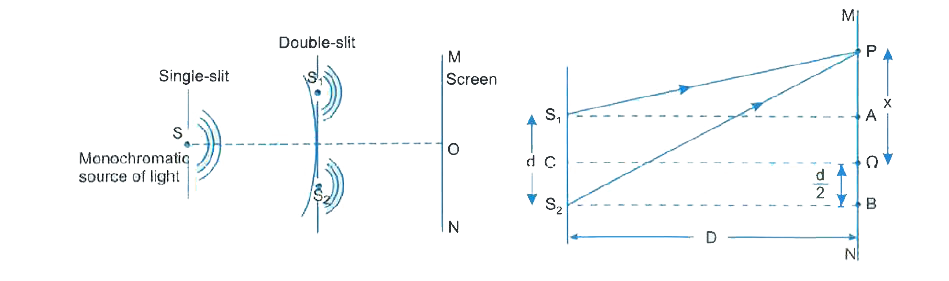
light waves reaching point P from two slit sources is `S_(2)P-S_(1)P`, where
`(S_(2)P)^(2)=D^(2)+(x+d/2)^(2)` and `(S_(1)P)^(2)=D^(2)+(x-d/2)^(2)`
`therefore(S_(2)P)^(2)-(S_(1)P)^(2)=[D^(2)+(x+d/2)^(2)]-[D^(2)+(x-d/2)^(2)]=2xd`
`rArr(S_(2)P-S_(1)P)(S_(2)p+S_(1)P)=2xd`
or `(S_(2)P-S_(1)P)=(2xd)/((S_(2)P+S_(1)P))`
If x and dare very very small as compared to D, then `(S_(2)P+S_(1)P)` may be considered as 2D. Hence,
`[S_(2)P-S_(1)P]=(2xd)/(2D)=(xd)/D`
For constructive interference, path difference must be an integer multiple of `lamda` i.e., `(xd)/D=nlamda` where n = 0, 1, 2, 3, ... etc.
`thereforex=(nDlamda)/d` i.e., positions of various maxima (bright bands) will be given by :
`x_(0)=0,x_(1)=(Dlamda)/d,x_(2)=(2Dlamda)/d,x_(3)=(3Dlamda)/d` ........
For destructive interference, path difference must be an odd multiple of `lamda/2` i.e., `(xd)/D=(2n-1)lamda/2`, where n ::= 1, 2, 3, ... etc.
`rArrx=((2n-1)Dlamda)/(2d)` i.e., positions of various minima (dark bands) will be given by :
`x_(1).=(Dlamda)/(2d),x_(2).=(3Dlamda)/(2d),x_(3).=(5Dlamda)/(2d)` ......
Fringe width of the fringe pattern is defined as the distance between two successive maxima or successive minima. Therefore, considering two successive maxima, we have
Fringe width `beta=x_(n+1)-x_(n)=((n+1)Dlamda)/d-(nDlamda)/d=(Dlamda)/d`
(b) Here wavelength`lamda`= 588 nm and refractive index of water w.r.t. air `n =4/3`
We know that speed of light in air =`c=3xx10^(8)ms^(-1)`
`therefore` Speed of light in water v =`c/n=(3xx10^(8))/((4//3))=2.25xx10^(8)ms^(-1)`
and wavelength of given light in water, `lamda_(w)=lamda/n=(588nm)/((4//3))=441nm`
