Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
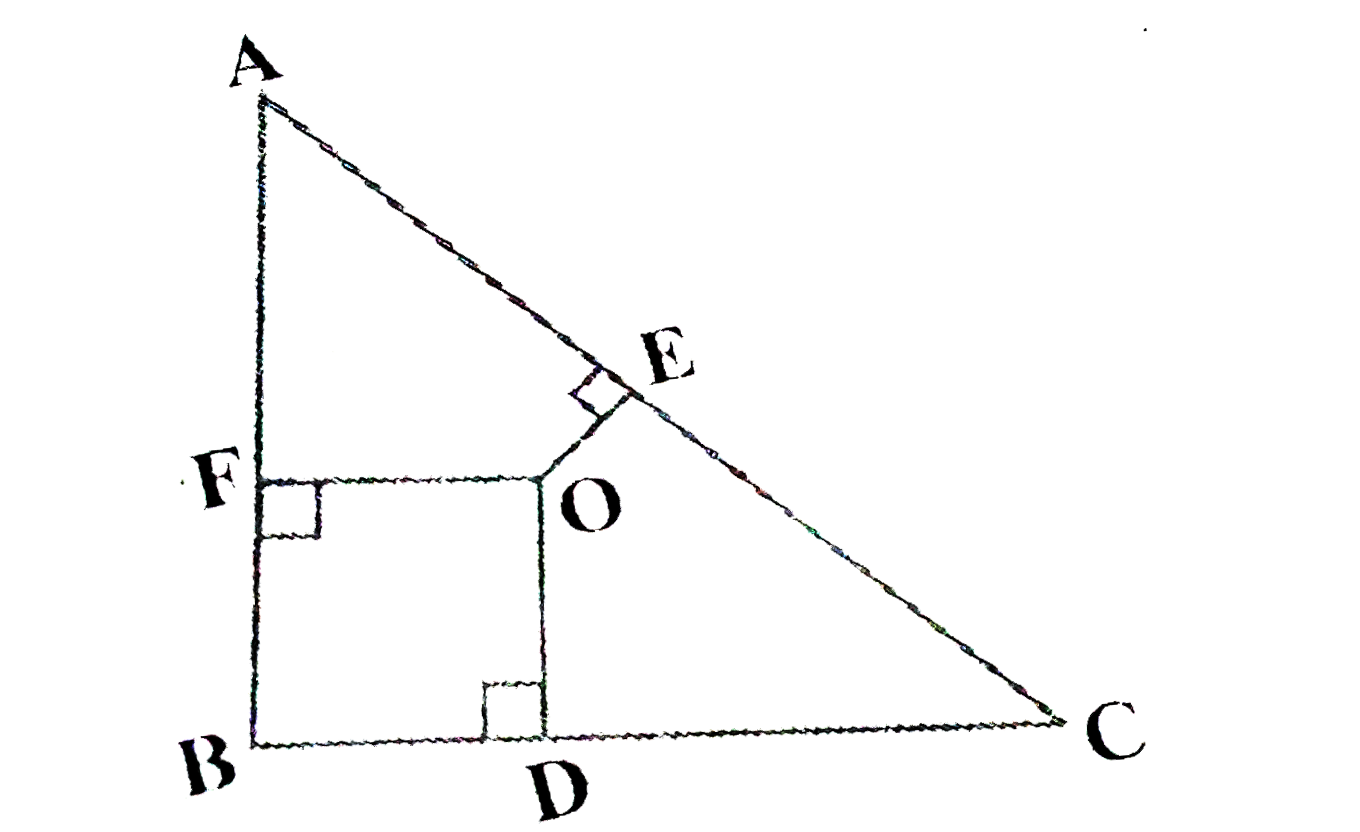
- In figure, O is a point in the interior of a triangle ABC, O D|B C ,O...
Text Solution
|
- In figure, O is a point in the interior of a triangle ABC, O D|B C ,O...
Text Solution
|
- If O\ a n d\ O^(prime) are circumcentre and orthocentre of \ A B C ,\ ...
Text Solution
|
- For the given cell Pt(D(2)|D^(o+))||H^(o+)|Pt(H(2)) , if E^(c-).(D(2)|...
Text Solution
|
- Which of the following pair would have larger size? a. K or K^(o+) , b...
Text Solution
|
- O is any point inside a rectangle ABCD. Prove that O B^2+O D^2=O A^2+...
Text Solution
|
- In figure, O is a point in the interior of a triangle ABC, O D|B C ,O...
Text Solution
|
- O is any point inside a triangle A B C . The bisector of /A O B ,/B O ...
Text Solution
|
- From a point O in the interior of a A B C , perpendiculars O...
Text Solution
|