Home
Class 9
MATHS
Show that in a right triangle the hyp...

Show that in a right triangle the hypotenuse is the longest side.

Text Solution

Verified by Experts


Let us consider a right-angled triangle ABC, right-angled at B.
In `∆ABC`,
`∠A + ∠B + ∠C = 180^@`(Angle sum property of a triangle)
...
Promotional Banner

Topper's Solved these Questions

  • TRIANGLES

    NCERT ENGLISH|Exercise EXERCISE 7.1|8 Videos

  • TRIANGLES

    NCERT ENGLISH|Exercise Solved Examples|9 Videos

  • TRIANGLES

    NCERT ENGLISH|Exercise EXERCISE 7.2|8 Videos

  • SURFACE AREAS AND VOLUMES

    NCERT ENGLISH|Exercise Exercise 13.9|3 Videos

Similar Questions

Explore conceptually related problems

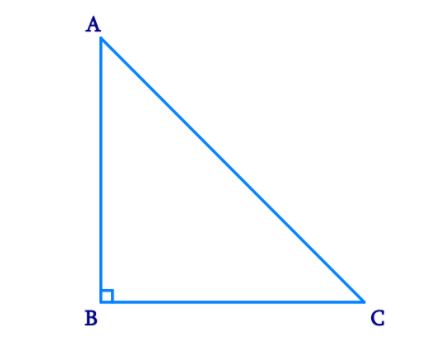
Show that in a right angled triangle, the hypotenuse is the longest side.

Find the area of a right triangle whose hypotenuse is 26 cm long and one of the sides containing the right angle measures 10 cm .

Theorem 6.7 : If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.

Equilateral triangles are drawn on the sides of a right triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.

Equilateral triangles are drawn on the sides of a right triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.

Find the area of a right triangle with hypotenuse of 10 and side of 8

(Pythagoras's Theorem) Prove by vector method that in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

(Pythagoras's Theorem) Prove by vector method that in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

If a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side of the perpendicular are similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse.

If a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side of the perpendicular are similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse.