Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two sides AB and BC and median AM of one triangle ABC are respectivel...
Text Solution
|
- If AD and PM are medians of triangles ABC and PQR, respectively where...
Text Solution
|
- Sides AB and AC and median AD of a triangle ABC are respectively prop...
Text Solution
|
- Sides AB and BC and median AD of a triangle ABC are respectively prop...
Text Solution
|
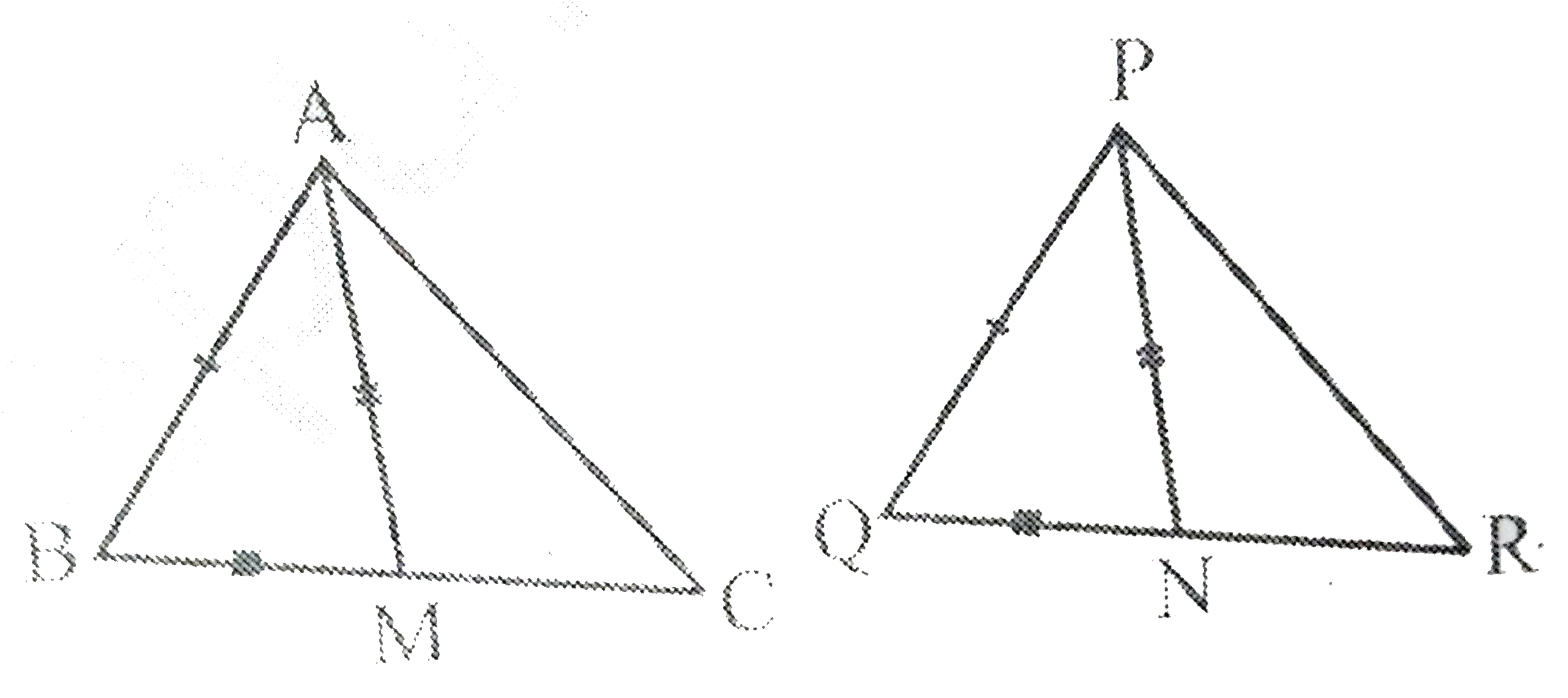
- In figure Cm and RN are respectively the medians of DeltaA B Cand De...
Text Solution
|
- Two sides AB and BC and median AM of one triangle ABC are respectivel...
Text Solution
|
- Two sides AB and BC and median AM of one triangle ABC are respectively...
Text Solution
|
- Two sides AB, BC and median AM of one triangle ABC are respectively eq...
Text Solution
|
- एक त्रिभुज ABC की दो भुजाए AB और BC तथा मध्यिका AM क्रमश: एक दुसरे त्र...
Text Solution
|