Similar Questions
Explore conceptually related problems
Recommended Questions
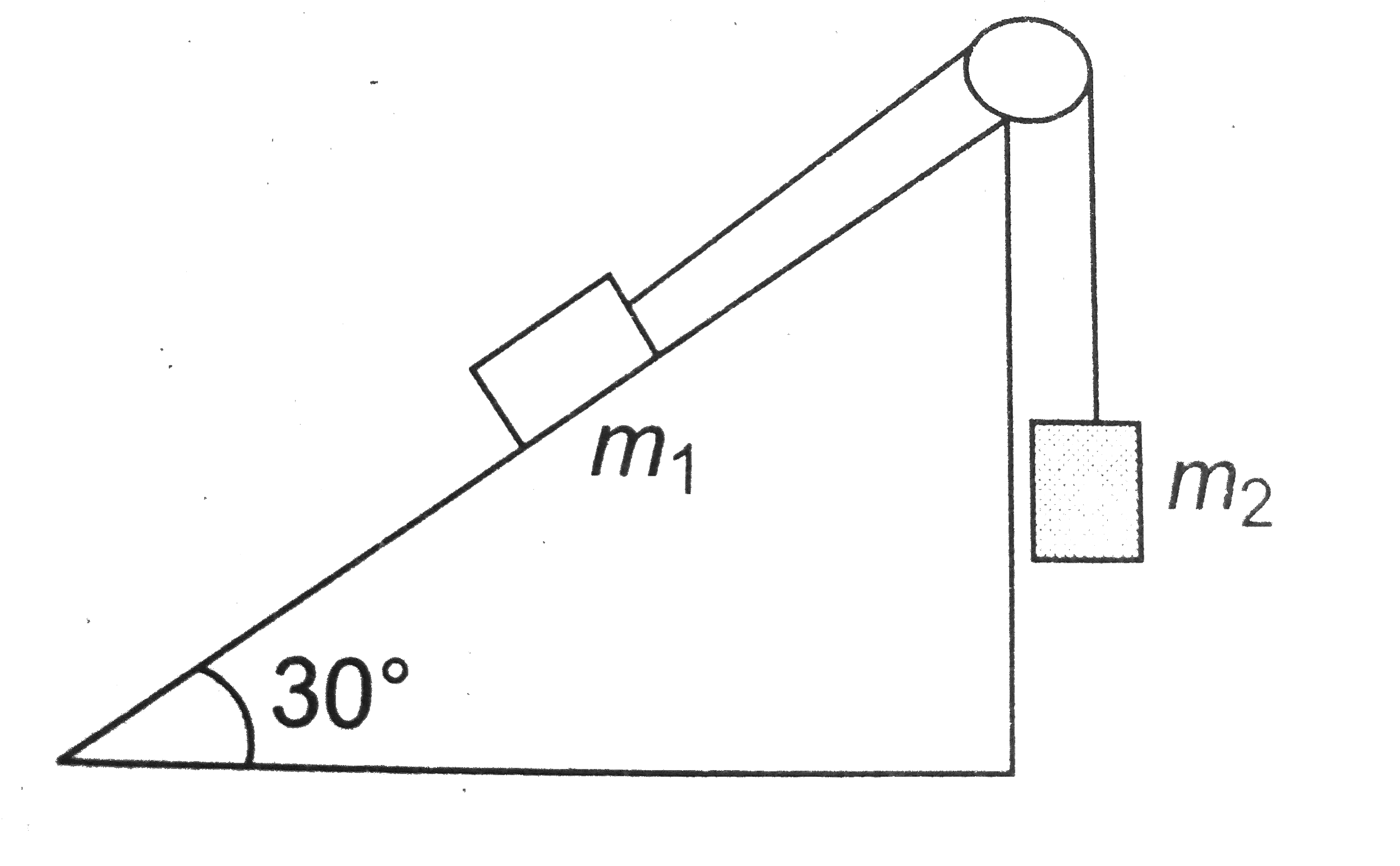
- M is a fixed wedge. Masses m(1) and m(2) are connected by a light stri...
Text Solution
|
- M is a fixed wedge. Masses m(1) and m(2) are connected by a light stri...
Text Solution
|
- Three blocks of masses m(1), m(2) and M are arranged as shown in figur...
Text Solution
|
- Two masses M(1) and M(2) connected by means of a string which is made ...
Text Solution
|
- Two masses m(1) and m(2) are connected by a light string passing over ...
Text Solution
|
- Two particles of mass m(1) and m(2)(m(1) gt m(2)) are attached to the ...
Text Solution
|
- Two masses m(1) and m(2) are attached to a string which passes over a ...
Text Solution
|
- Two masses m(1) and m(2) ( m(2) gt m(1)) are hanging vertically over f...
Text Solution
|
- A light string passing over a smooth light pulley connects two blocks ...
Text Solution
|