Similar Questions
Explore conceptually related problems
Recommended Questions
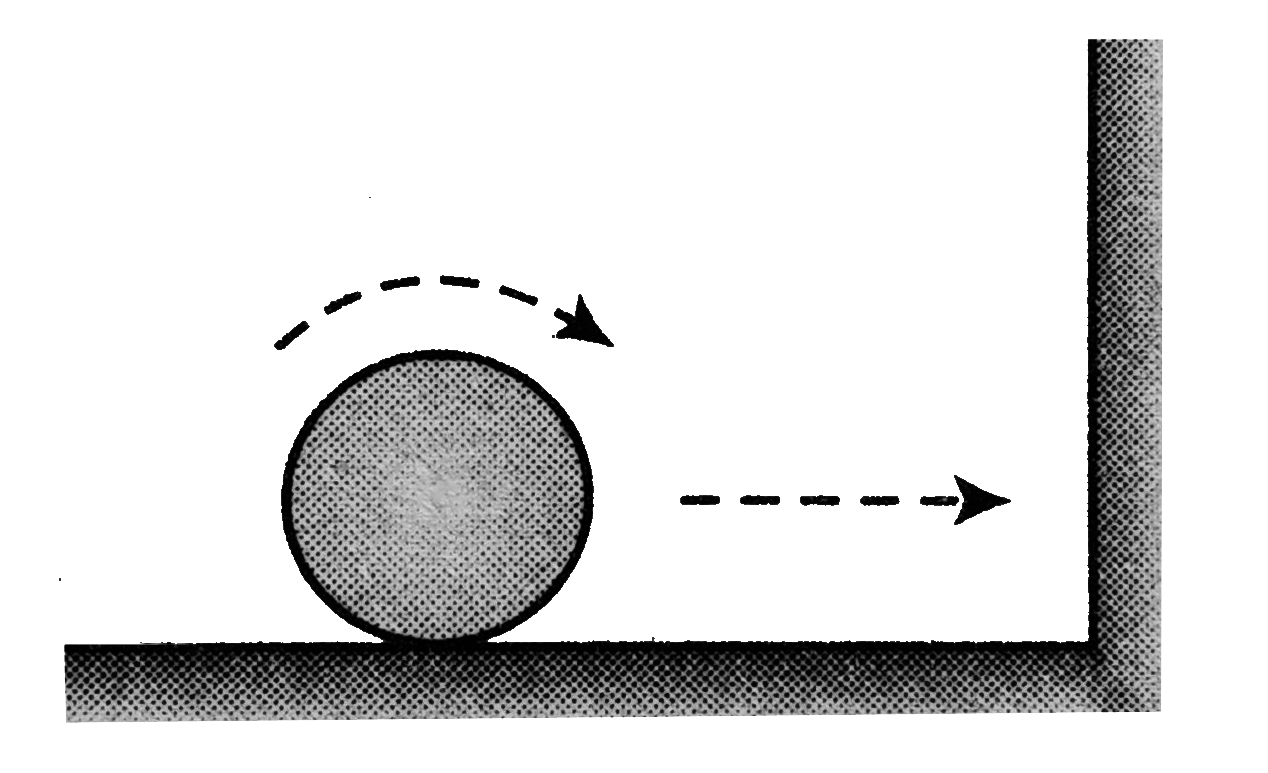
- A ball, rolling purely on a horizontal floor with centre's speed v, hi...
Text Solution
|
- A solid sphere rolls without slipping on a rough horizontal floor, mov...
Text Solution
|
- The ball of mas m moves with speed v againest a smooth , fixed vertica...
Text Solution
|
- A solid sphere rolls without slipping on a rough horizontal floor, mov...
Text Solution
|
- A ball, rolling purely on a horizontal floor with centre's speed v , h...
Text Solution
|
- A ball, rolling purely on a horizontal floor with centre's speed v, hi...
Text Solution
|
- Two balls each of mass 'm' are moving with same velocity v on a smooth...
Text Solution
|
- A ball is projected on a very long floor. There may be two conditions ...
Text Solution
|
- A uniform solid sphere of mass m, radius R moving with velocity v0 is...
Text Solution
|