Similar Questions
Explore conceptually related problems
Recommended Questions
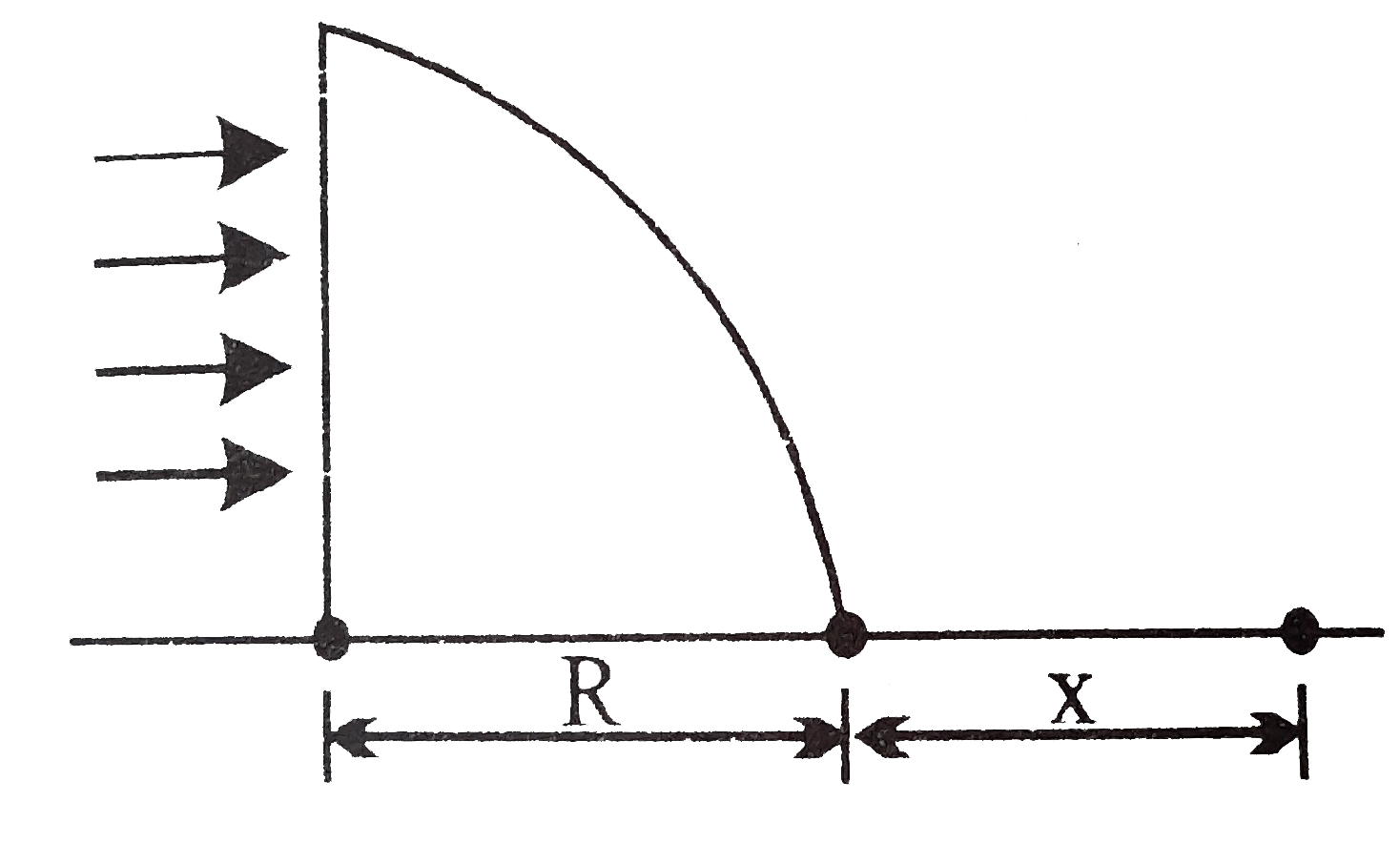
- A uniform,horizontal beam of light is incident upon a quarter cylinder...
Text Solution
|
- A light beam of diameter sqrt(3R) is incident symmetrically on a glass...
Text Solution
|
- A uniform,horizontal beam of light is incident upon a quarter cylinder...
Text Solution
|
- A quarter cylinder of radius R and refractive index 1.5 is placed on a...
Text Solution
|
- A uniform, horizontal parallel beam of light is incident upon a prism ...
Text Solution
|
- Quarter part of a transparent cylinder ABC of radius R is kept on a ho...
Text Solution
|
- A glass prism in the shape of a quarter cylinder lies on a horizontal ...
Text Solution
|
- अपवर्तनांक 1.5 तथा त्रिज्या R के एक सिलिंडर का चतुर्थांश मेज पर रखा गय...
Text Solution
|
- A uniform, horizontal beam of light is incident upon a quarter cyclind...
Text Solution
|