Text Solution
Verified by Experts
Topper's Solved these Questions
MOTION IN A PLANE
AAKASH SERIES|Exercise EXERCISE-A (Vectors & Scalars)|25 VideosMOTION IN A PLANE
AAKASH SERIES|Exercise EXERCISE-A (Addition & Subtractions of Vectors)|10 VideosMAGNETISM
AAKASH SERIES|Exercise PROBLEMS (LEVEL-II)|13 VideosMOTION IN A PLANE
AAKASH SERIES|Exercise QUESTION FOR DESCRIPTIVE ANSWER|7 Videos
Similar Questions
Explore conceptually related problems
AAKASH SERIES-MOTION IN A PLANE-EXERCISE-3 (Circular Motion)
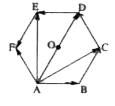
- ABCDEF is a regular hexagon with point O as centre. Find the value of ...
Text Solution
|
- A particle ‘P is moving in a circle of radius "r" with uniform speed v...
Text Solution
|
- Starting from rest a wheel rotates with uniform angular acceleration 2...
Text Solution
|
- A cyclist riding with a speed of 27 kmph. As he approaches a circular ...
Text Solution
|
- A particle is moving along a circular path in xy-plane. When it crosse...
Text Solution
|
- A particle moves on a circle of radius r with centripetal acceleration...
Text Solution
|
- The position vector of a particle vecR as a function of time is given ...
Text Solution
|
- A particle moves in a circular path such that its speed v varies with...
Text Solution
|