Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ZEN PUBLICATION-TRIANGLES-ZEE ADDITIONAL QUESTIONS - LONG ANSWER TYPE QUESTIONS
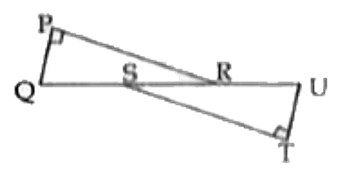
- In the figure lfloorQPR=lfloorUTS=90^(@)andPR||TS. Prove that DeltaPQR...
Text Solution
|
- Throught the mid-point M of the sides of a parallelogram ABCD, the li...
Text Solution
|
- A 5 m long ladder is placed leaning towards a vertical wall such that ...
Text Solution
|
- In the figure, OB is the perpendicular bisector of the line segment DE...
Text Solution
|
- In triangle ABC, AP, BQ and CR are the medians. Prove that 3[AB^(2)+BC...
Text Solution
|
- If A is the area of a right angled triangle and b is one of the sides ...
Text Solution
|
- In the given figure, AD is the median of DeltaABCandAE|BC. Prove that ...
Text Solution
|
- In an equilateral triangle ABC, D is a point of BC such that 4BD = BC....
Text Solution
|
- Prove that the ratio of the areas of two similar triangles is equal to...
Text Solution
|
- In a right angled triangle, square on the hypotenuse is equal to sum o...
Text Solution
|
- State and prove pythagoras theorem .
Text Solution
|