Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the maximum and minimum distances of the planet A from the sun S...
Text Solution
|
- Find the maximum and minimum distances of the planet A from the sun S...
Text Solution
|
- A planet of mass m revolves in elliptical orbit around the sun of mass...
Text Solution
|
- A planet of mass m moves around the Sun of mass Min an elliptical orbi...
Text Solution
|
- A point moves along an arc of a circle of radius R. Its velocity depen...
Text Solution
|
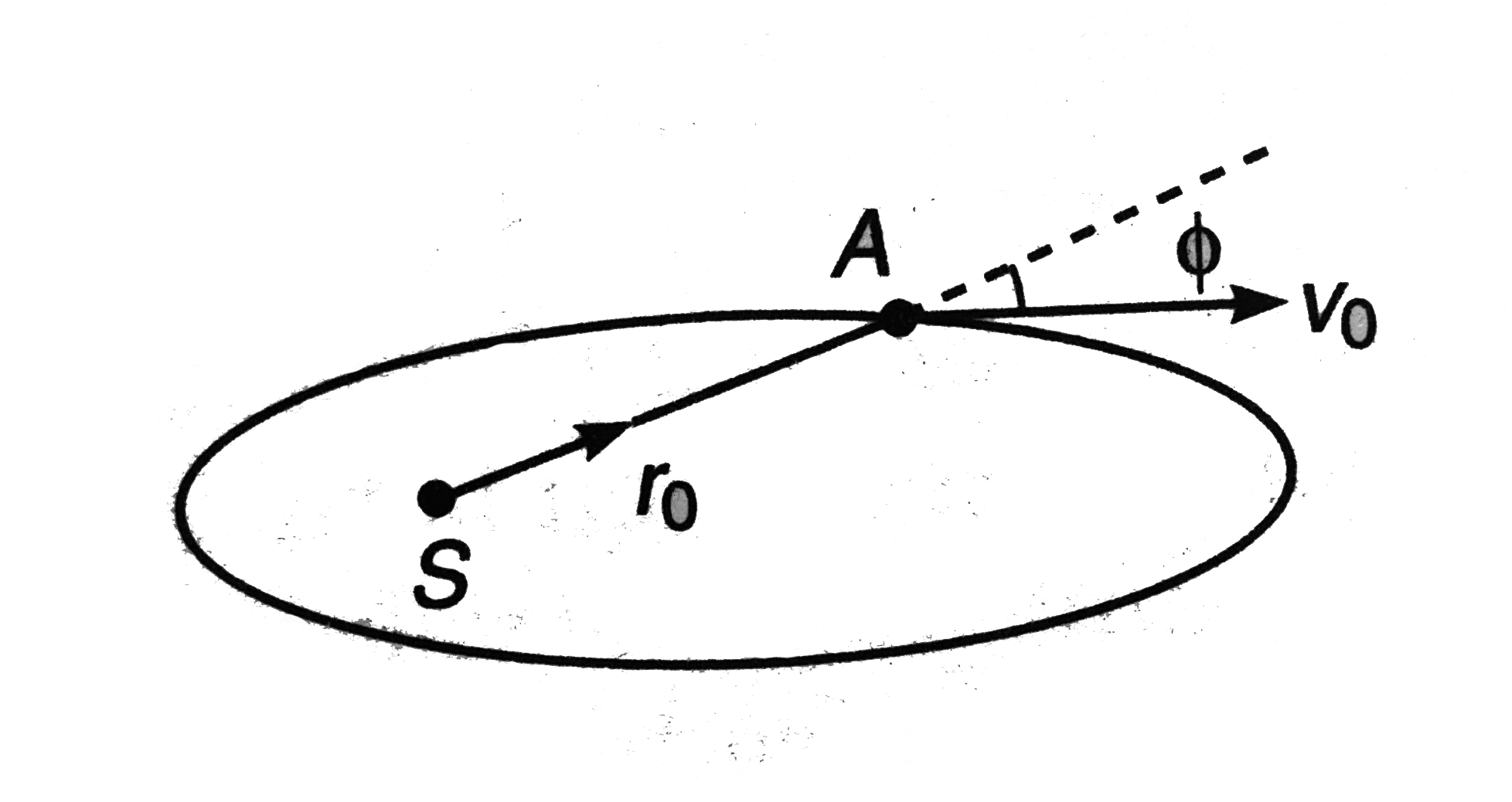
- A planet A moves along an elliptical orbit around the Sun. At the mome...
Text Solution
|
- The radius vector drawn from the sun to a planet sweeps outareas in eq...
Text Solution
|
- A planet goes around the sun in an elliptical orbit. The minimum dista...
Text Solution
|
- If a planet revolve around the sun in an elliptical orbit such that it...
Text Solution
|