Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
OSWAAL PUBLICATION-II PUC MARCH - 2018-PART - D
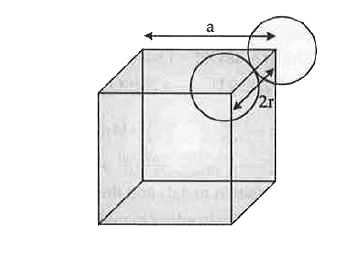
- An element having atomic mass 107.9 u has FCC lattice. The edge length...
Text Solution
|
- The boiling point of benzene is 353.23 K when 1.80 g of a non-volatile...
Text Solution
|
- i) State Kohlrausch law. ii) What is meant by limiting molar conduct...
Text Solution
|
- Derive an integrated rate equation for the rate constant of a first-or...
Text Solution
|
- What is heterogeneous catalysis? Give an example.
Text Solution
|
- Name the reagent used in the dehydrohalogenation of haloalkanes.
Text Solution
|
- Write the mechanism of aicd catalysed dehydration of ethanol to ethane...
Text Solution
|
- How does propanone (CH(3)COCH(3)) reacts with hydrazine? Give equatio...
Text Solution
|
- (a) Explain carbyl amine reaction with equation. (b) How does nitrob...
Text Solution
|
- (a) Write Haworth structure of "Lactose". (b) i) What are non-essent...
Text Solution
|
- (a) Explain the preparation of Nylon-6, 6 with equation. (b) What ar...
Text Solution
|