A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CIRCLES
OSWAAL PUBLICATION|Exercise VERY SHORT ANSWER TYPE QUESTIONS|11 VideosCIRCLES
OSWAAL PUBLICATION|Exercise SHORT ANSWER TYPE QUESTIONS|4 VideosARITHMETIC PROGRESSIONS
OSWAAL PUBLICATION|Exercise TEXTBOOK CORNER EXERCISE 1.4|5 VideosCO-ORDINATE GEOMETRY
OSWAAL PUBLICATION|Exercise TEXTBOOK CORNER (EXERCISE 7.4)|7 Videos
Similar Questions
Explore conceptually related problems
OSWAAL PUBLICATION-CIRCLES -TEXTBOOK CORNER (EXERCISE 4.2)
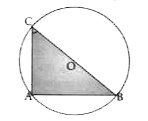
- O is the centre of a circle ,AB is a chord .From the figure ,angleACB ...
Text Solution
|
- From a point Q ,the length of the tangent to a circle is 24 cm and the...
Text Solution
|
- In the Fig, if TP and TQ are the two tangents to a circle with centre...
Text Solution
|
- If tangents PA and PB from a point P to a circle with centre O are inc...
Text Solution
|
- Prove that the tangents drawn at the ends of a diameter fo a circle ar...
Text Solution
|
- Prove that the perpendicular at the point of contact to the tangen...
Text Solution
|
- The length of a tangent from a point A at distance 5 cm from the centr...
Text Solution
|
- Two concentric circle of radii 5 cm and 3cm are drawn. Find the length...
Text Solution
|
- A quadrilateral ABCD is drawn to circumscribe a circle (see Figure).Pr...
Text Solution
|
- In the given figure ,XY and XY are two parallel tangents to a circle w...
Text Solution
|
- Prove that the angle between the two tangents drawn from an external p...
Text Solution
|
- Prove that the parallelogram circumscribing a circle is a rhombus.
Text Solution
|
- A triangle ABC is drawn to circumscribe a circle of radius 4 cm such t...
Text Solution
|
- Prove that opposites of a quadrilaterial circumscribing a circle subte...
Text Solution
|