Home
Class 10
MATHS
The angle of elevation of the top of a t...

The angle of elevation of the top of a tower of height "h" metres from two points at a distance of "a" and "b" metres from the base and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)` meters.

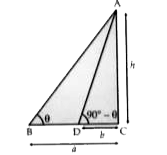
Text Solution

Verified by Experts

The correct Answer is:
`sqrt(ab)` metres.
Promotional Banner

Topper's Solved these Questions

  • SOME APPLICATION OF TRIGONOMETRY

    OSWAAL PUBLICATION|Exercise LONG ASNWER TYPE QUESTIONS-II|1 Videos

  • SOME APPLICATION OF TRIGONOMETRY

    OSWAAL PUBLICATION|Exercise TEXTBOOK CORNER EXERCISE 12.1|16 Videos

  • SOME APPLICATION OF TRIGONOMETRY

    OSWAAL PUBLICATION|Exercise SHORT ASNWER TYPE QUESTIONS|2 Videos

  • SOLVED PAPER SSLC KARNATAKA JUNE 2020

    OSWAAL PUBLICATION|Exercise Answer the following questions |37 Videos

  • SSLC KARNATAKA TOPPERS' ANSWERS MARCH 2018 Class-X

    OSWAAL PUBLICATION|Exercise SECTION-E |4 Videos

Similar Questions

Explore conceptually related problems

The angle of elevation of the top of a tower from two points at a distance of 4m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.

If the angle of elevation of a tower from two points distant a and b (a lt b) from its foot and on the same straight line from it is 30^(@) and 60^(@) , the height of the tower is

If the angle of elevation of the top of a tower from a distance of 100m from its foot is 60^(@) , the height of the tower is

The angle of elevation of the top of a tower from a point of the ground, which is 30 m away from the foot of a tower of height 10sqrt3 , is:

The angle of elevation of the top of a hill from each of the vertices A, B, C of a horizontal triangle is α. The height of the hill is :

The angle of elevation of the top of a tower from a point O on the ground, qhich is 450 m away from the foot of the tower, is 40^(@) . Find the height of the tower.

The angle of elevation of the top of a tower from a point on the groud, which is 30 m away from the foot of the tower is 30^(@) . Find the height of the tower.

The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30^(@) . Find the height of the tower.