Similar Questions
Explore conceptually related problems
Recommended Questions
- A square of side a and uniform thickness is divided into four equal pa...
Text Solution
|
- A square of side 2cm and uniform thickness is divided into four square...
Text Solution
|
- A square of side a and uniform thickness is divided into four equal pa...
Text Solution
|
- A square of side 4 m having uniform thickness is divided into four equ...
Text Solution
|
- In the figure shown a semicircular area is removed from a uniform squa...
Text Solution
|
- Fron a sqaure plate of side a,a quarter circular disc of radius a is r...
Text Solution
|
- From a uniform square plate, one-fourth part is removed as shown. The ...
Text Solution
|
- 4R प्रतिरोध के एक तार को चार बराबर भागो में विभक्त किया जाता है। तत्पश...
Text Solution
|
- a is divided into two such parts that one part is equal to the square ...
Text Solution
|
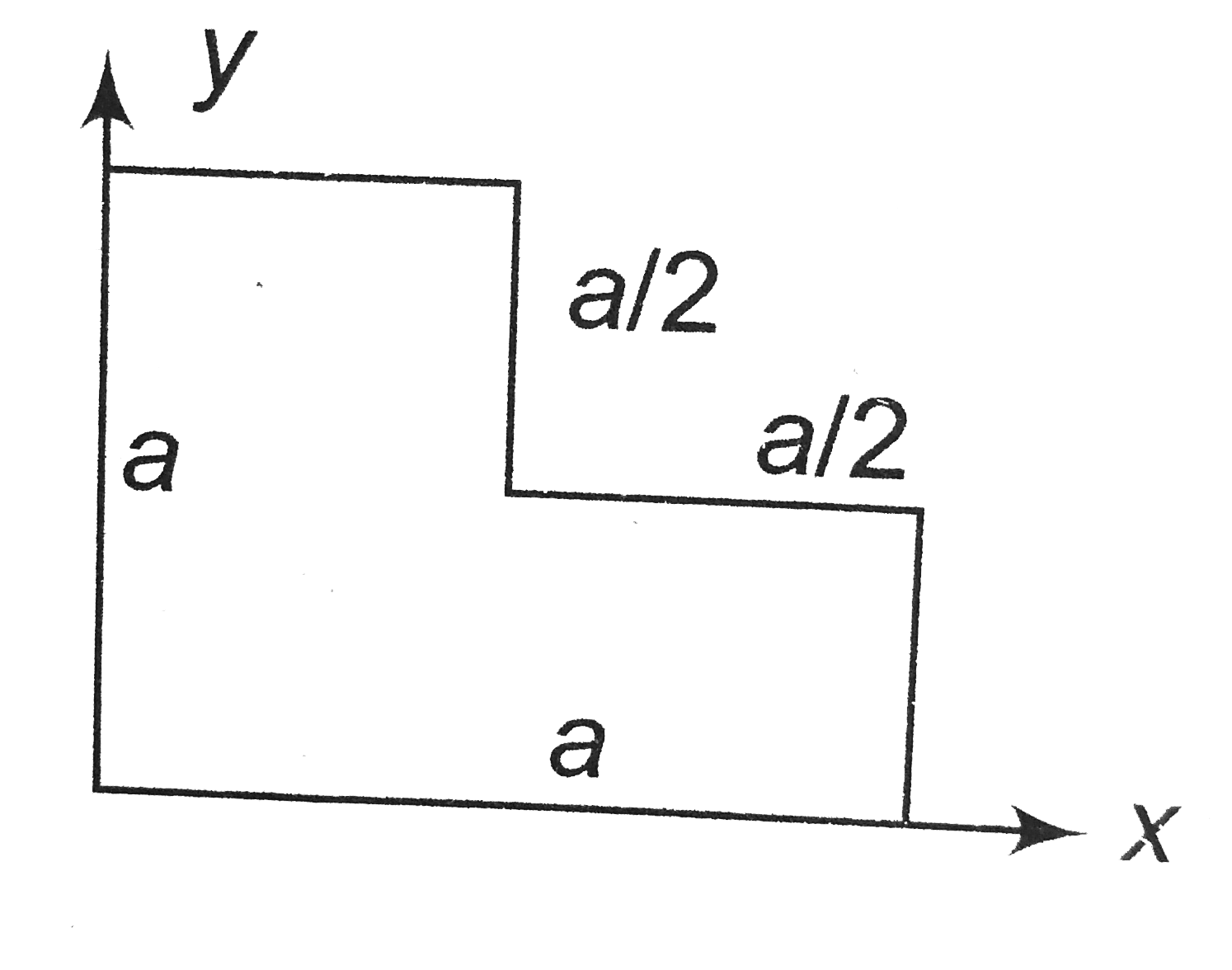 .
.