Similar Questions
Explore conceptually related problems
Recommended Questions
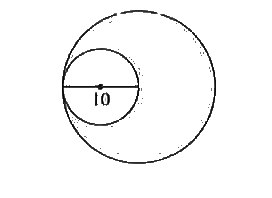
- The figure below shows 2 tangent circles such that the 10-centimeter d...
Text Solution
|
- Determine the point of symmetry of a regular hexagon. <img src="htt...
Text Solution
|
- Find the area of the shaded region, given that the radius of each circ...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Find the area of figure given below.
Text Solution
|
- Find the perimeter of the figure given below.
Text Solution
|
- Find the area of the figure given below.
Text Solution
|