Similar Questions
Explore conceptually related problems
Recommended Questions
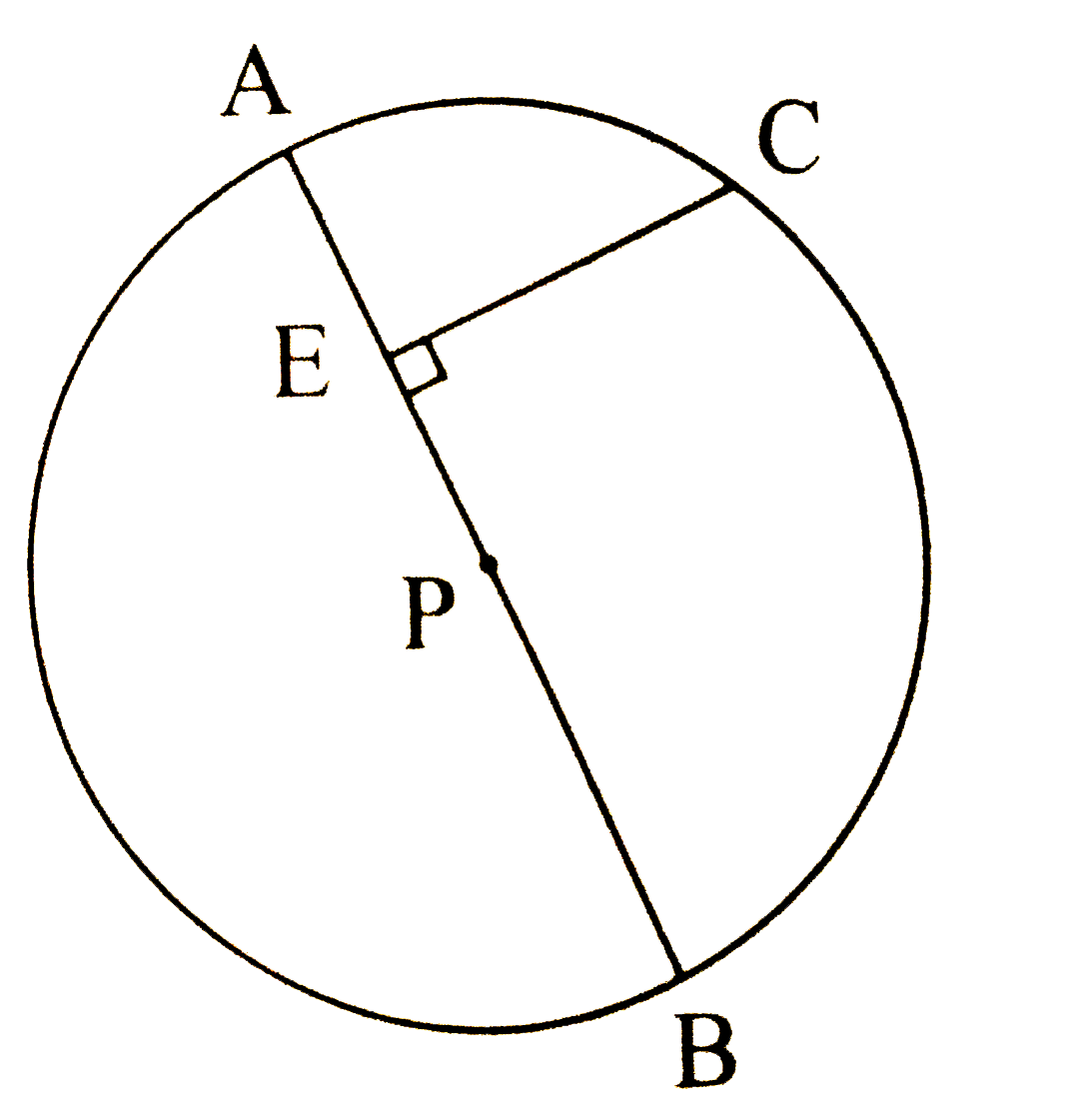
- In the above figure, seg AB is a diameter of a circle with centre P.C ...
Text Solution
|
- Theorem of external division of chords. If secants containing chords...
Text Solution
|
- In the figure, seg AB~= seg AC, ray CE bisects /ACB , ray BD bisects /...
Text Solution
|
- In the figure, seg AB is a diameter of a circle with centre C. Line PQ...
Text Solution
|
- In the above figure, seg AB is a diameter of a circle with centre P.C ...
Text Solution
|
- Chords AB and CD of a circle intersect inside the circle at point E. I...
Text Solution
|
- In DeltaABC,ray BD bisects angleABC and ray CE bisects angleACB. If se...
Text Solution
|
- In the adjoining figure , circles with centres C and D touch internall...
Text Solution
|
- In the adjoining figure, seg AB is a diameter of a circle with centre ...
Text Solution
|