Similar Questions
Explore conceptually related problems
Recommended Questions
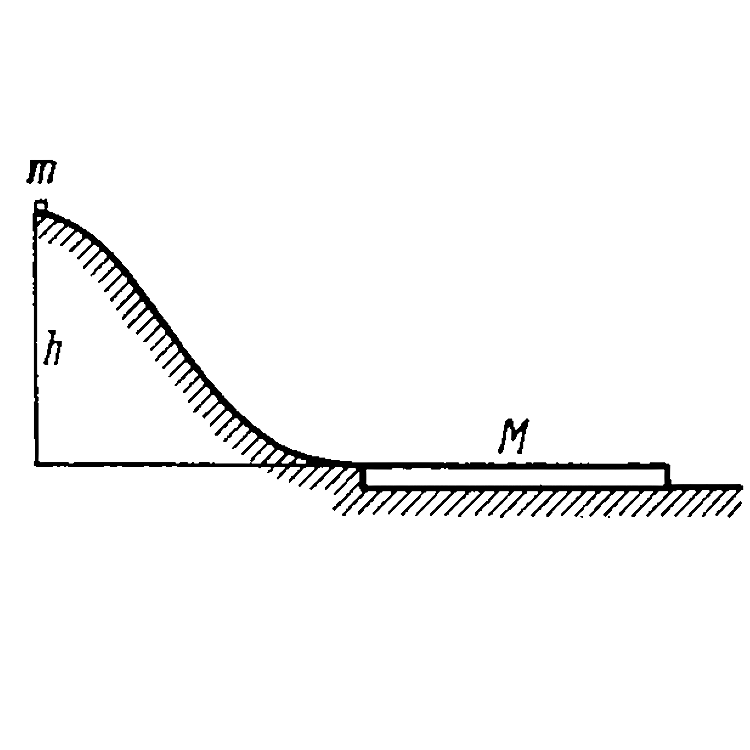
- A small disc of mass m slides down a smooth hill of height h without i...
Text Solution
|
- A solid uniform disc of mass m rols without slipping down a fixed incl...
Text Solution
|
- A small disc of mass m slides down a smooth hill of height h without i...
Text Solution
|
- In the figure shown, a solid sphere of mass 'm' and radius r is releas...
Text Solution
|
- A disc of mass m and radius R is placed over a plank of same mass m. T...
Text Solution
|
- A disc of mass m and radius R is placed over a plank of same mass m. T...
Text Solution
|
- A uniform disc of mass M and radius R initially stands vertically on t...
Text Solution
|
- A uniform disc of mass M and radius R initially stands vertically on t...
Text Solution
|
- A uniform disc of mass M and radius R initially stands vertically on t...
Text Solution
|