Similar Questions
Explore conceptually related problems
Recommended Questions
- A disc of radius R and mass M is rolling horizontally without slipping...
Text Solution
|
- A disc of radius R and mass M is rolling horizontally without slipping...
Text Solution
|
- A solid cylinder of mass M and radius R rolls down an inclined plane o...
Text Solution
|
- A sphere of mass m and radius r rolls on a horizontal plane without sl...
Text Solution
|
- A metal disc of radius R and mass M freely rolls down from the top of ...
Text Solution
|
- A ring, disc, spherical shell and solid sphere of same mass and radius...
Text Solution
|
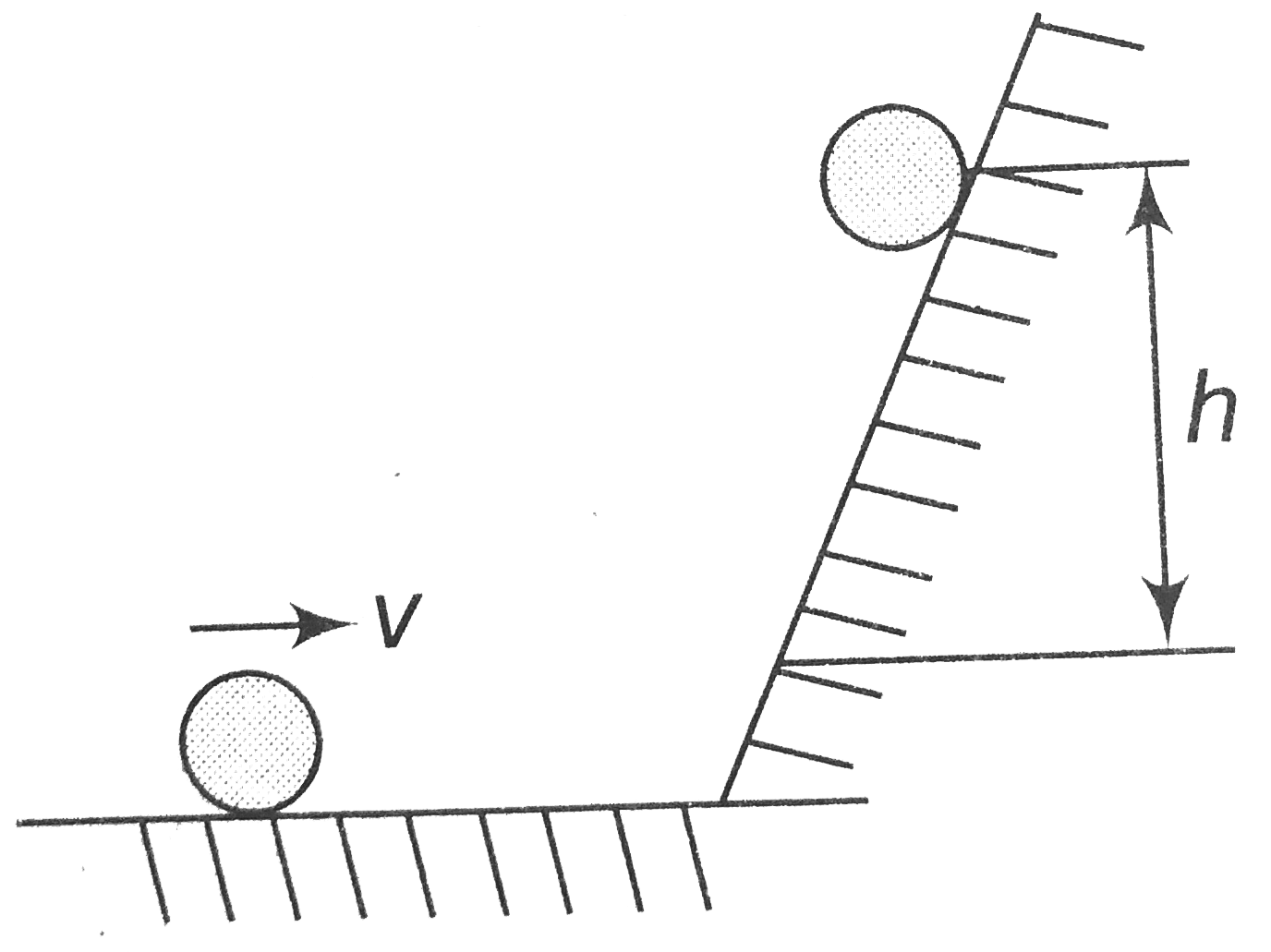
- A disc of mass M and radius R rolls on a horizontal surface and then r...
Text Solution
|
- A disc of mass M and radius R rolls on a horizontal surface and then r...
Text Solution
|
- A sphere of mass m and radius r rolls on a horizontal plane without sl...
Text Solution
|
 .
.