Similar Questions
Explore conceptually related problems
Recommended Questions
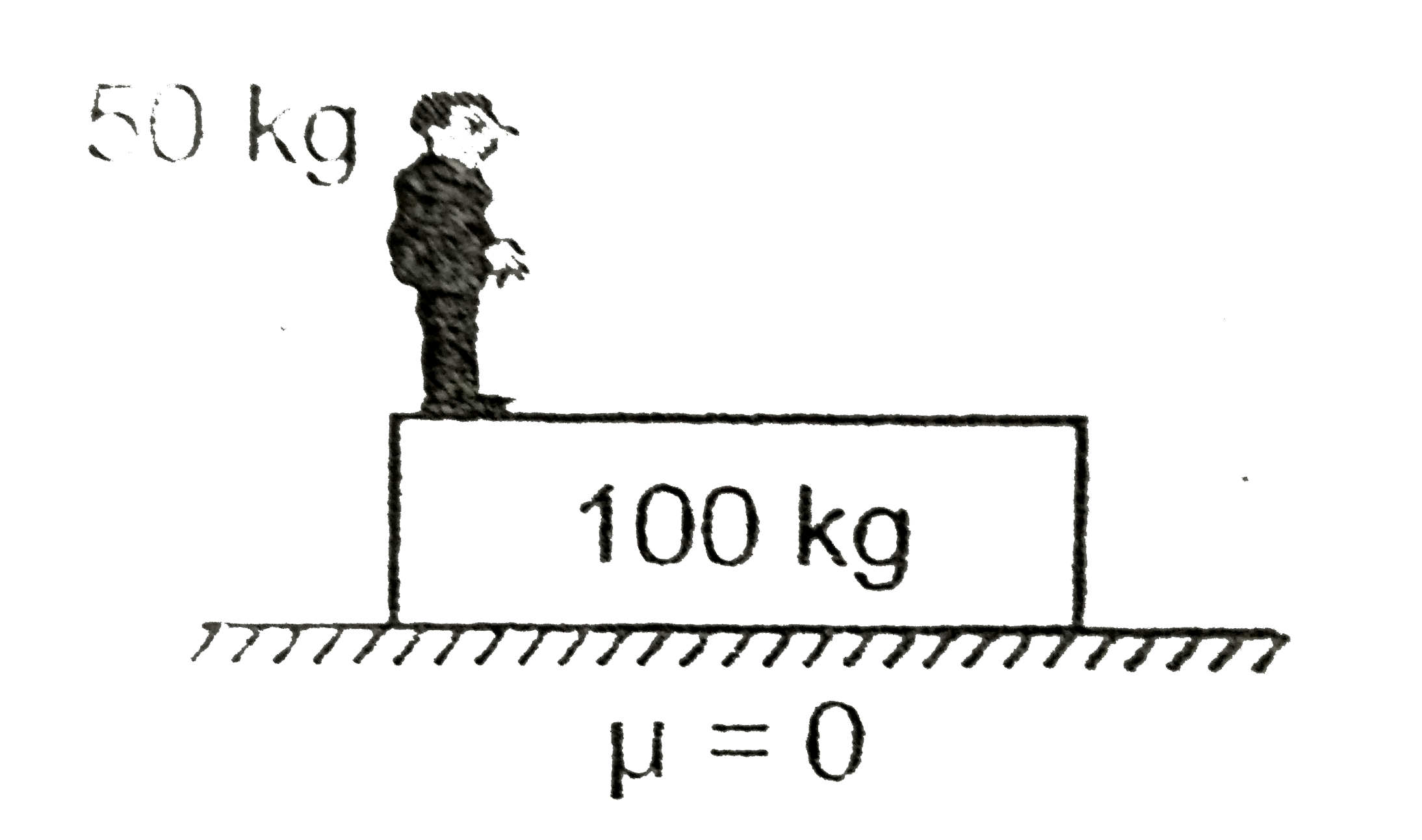
- A man of mass 50 kg us standing on a 100 kg plank kept on a fricitonle...
Text Solution
|
- No external force: Stationery mass relative to an inertial frame remai...
Text Solution
|
- A man of mass 80 kg stands on a plank of mass 40 kg. The plank is lyin...
Text Solution
|
- A man of mass M stands at one end of a stationary plank of length L, l...
Text Solution
|
- A man of mass m is standing on a plank of equal mass m resting on a sm...
Text Solution
|
- A man of mass 50 kg is pulling on a plank of mass 100 kg kept on a smo...
Text Solution
|
- A man of mass 50 kg us standing on a 100 kg plank kept on a fricitonle...
Text Solution
|
- A wooden plank of mass 20 kg is resting on a smooth horizontal floor. ...
Text Solution
|
- A man of mass M stands at one end of a plank of length L Which lies at...
Text Solution
|