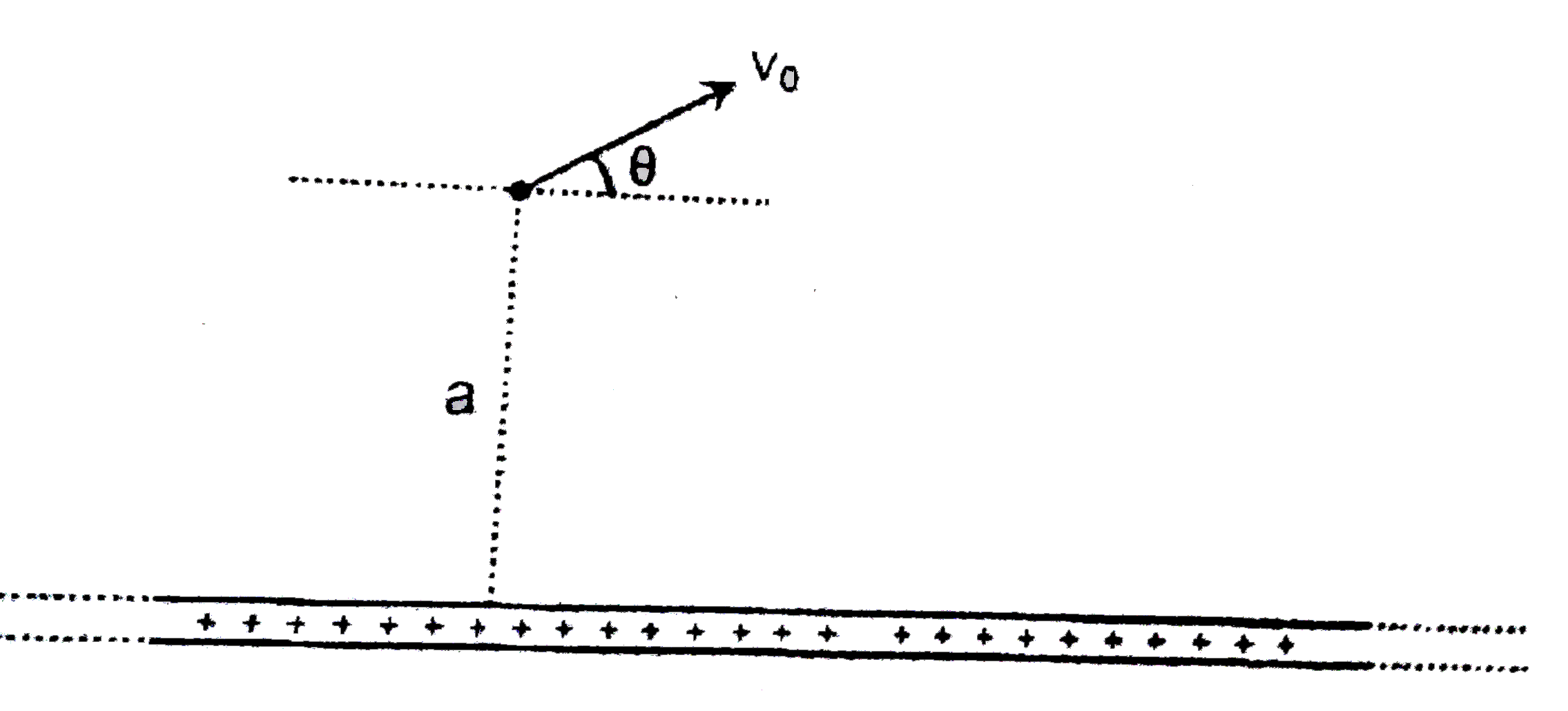Similar Questions
Explore conceptually related problems
Recommended Questions
- There is an infinite line of uniform linear density of charge +lamda. ...
Text Solution
|
- A charge particle q is released at a distance R(@) from the infinite l...
Text Solution
|
- A particle of mass m carrying charge q is projected with velocity v fr...
Text Solution
|
- In the figure shown there is a large sheet of charge of uniform surfac...
Text Solution
|
- A long straight wire carries a charge with linear density lamda . A pa...
Text Solution
|
- There is an infinite line of uniform linear density of charge +lamda ....
Text Solution
|
- An infinite line cahrge is perpendicular to the plane of the figure ha...
Text Solution
|
- A particle P of charge q and m , is placed at a point in gravity free ...
Text Solution
|
- An infinite line charge produces a field of 4.5xx10^(4) N//C at a dist...
Text Solution
|