Similar Questions
Explore conceptually related problems
Recommended Questions
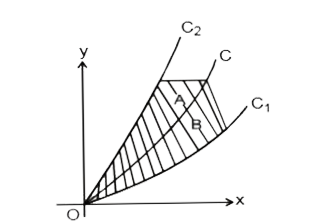
- Let C(1 )and C(2) be two curves passing through the origin as shown in...
Text Solution
|
- The equation of a circle C1 is x^2+y^2= 4. The locus of the intersec...
Text Solution
|
- Consider two curves C1:y =1/x and C2.y=lnx on the xy plane. Let D1, de...
Text Solution
|
- Consider two curves C(1):y=(1)/(x) and C(2),y=ln x on the xy plane.Let...
Text Solution
|
- Consider two curves C(1):y=(1)/(x) and C(2),y=ln x on the xy plane.Let...
Text Solution
|
- Consider two curves C(1):y=(1)/(x) and C(2),y=ln x on the xy plane.Let...
Text Solution
|
- Let C be the set of curves having the property that the point of inter...
Text Solution
|
- दो वक्र c(1)=y^(2)=4x व c(2)=x^(2)+y^(2)-6x+1=0 हैं, तब-
Text Solution
|
- Let C(1 )and C(2) be two curves passing through the origin as shown in...
Text Solution
|