Similar Questions
Explore conceptually related problems
Recommended Questions
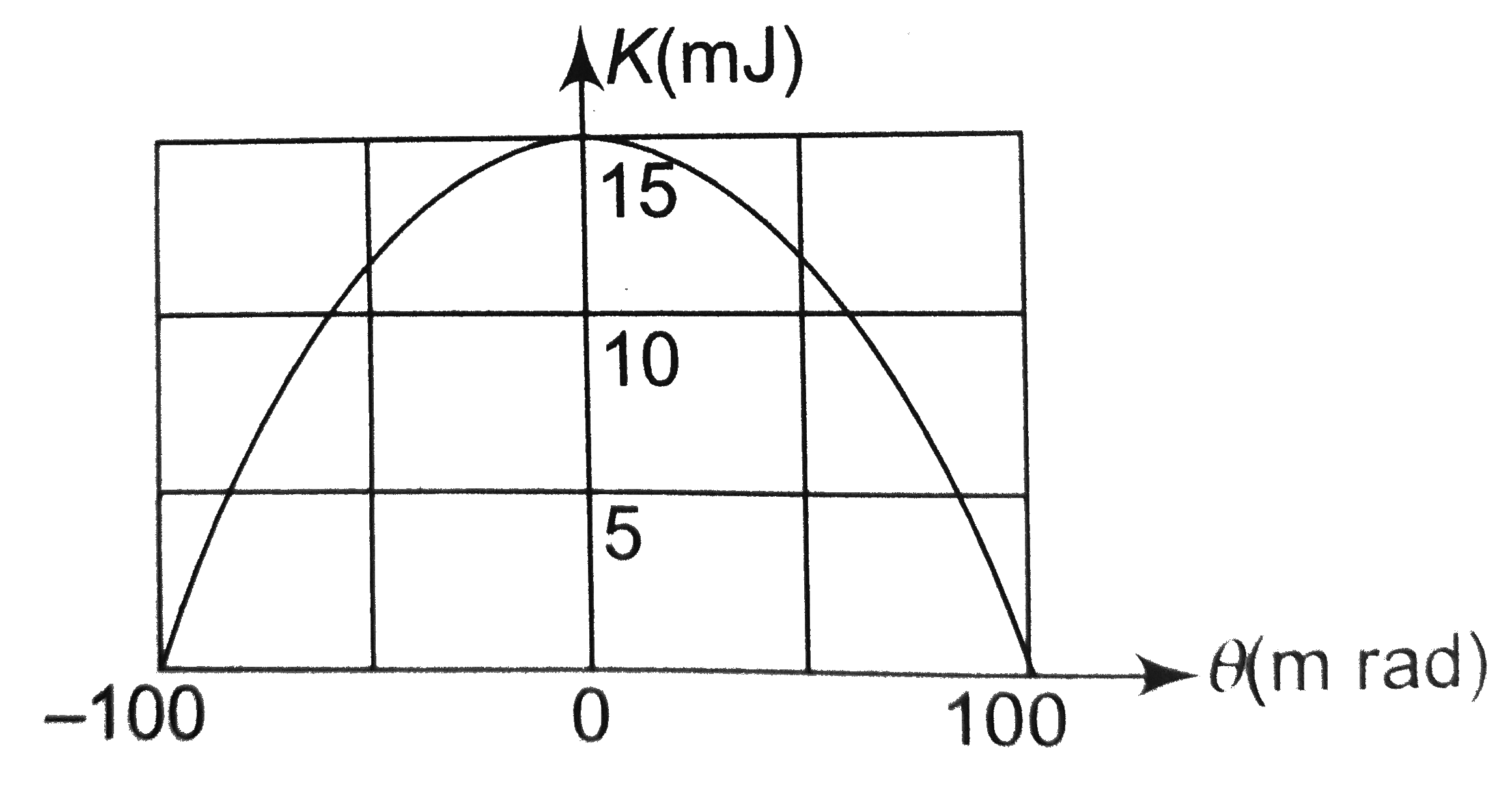
- Figure shown the kinetic energy K of a pendulum versus. its angle thet...
Text Solution
|
- A simple pendulum of length l has maximum angular displacement theta ....
Text Solution
|
- Figure shown the kinetic energy K of a pendulum versus. its angle thet...
Text Solution
|
- A 1N pendulum bob is held at an angle theta from the vertical by a 2N ...
Text Solution
|
- A simple pendulum of length l has a maximum angular displacement theta...
Text Solution
|
- Figure shows the kinetic energy K of a simple pendulum versus its angl...
Text Solution
|
- A simple pendulum of length I and mass (bob) m is suspended vertically...
Text Solution
|
- A simple pendulum is released from A as shown. If m and 1 represent th...
Text Solution
|
- 5.0muC आवेश वाला द्रव्यमान 2g का एक सरल लोलक का बॉब तीव्रता 2000V//m क...
Text Solution
|