Read the following passage carefully and answer the questions

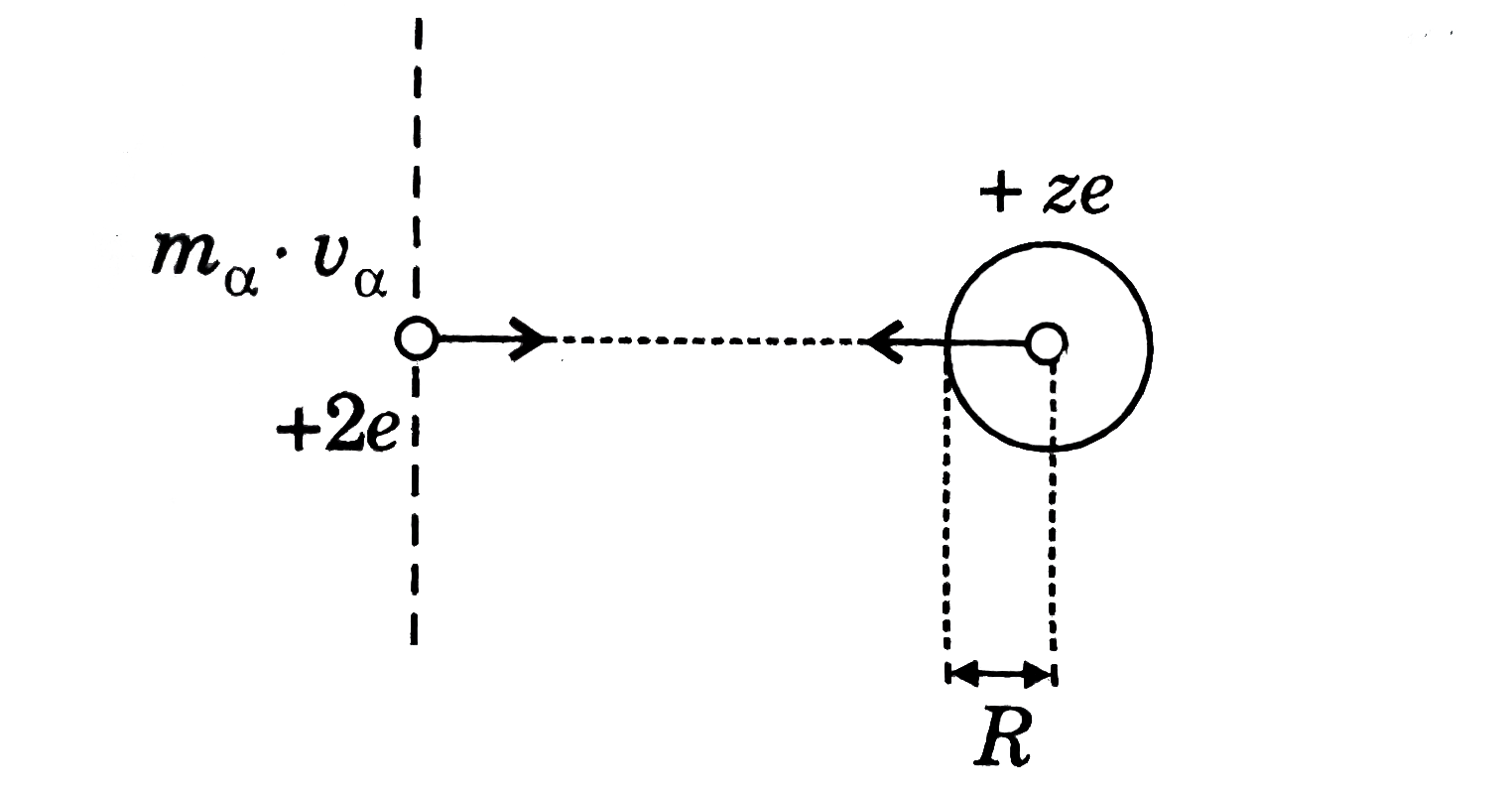
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's `alpha-`scattering experiment. If an `alpha-`perticle is projected from infinity with speed v, towards the nucleus having z protons then the `apha-`perticle which is reflected back or which is deflected by `180^(@)` must have approach closest to the nucleus. It can be approximated that `alpha-`particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
`("Total Energy")_("initial") = ("Total Enregy")_("final")`
`(KE)_(i) +(PE)_(i)=(KE)_(f)+(PE)_(f)`
`(PE)_(i) =0, "since"PE` of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
`1/2m_(alpha)v_(alpha)^(2) + 0=0 + (kq_(1)q_(2))/(R)`
`rArr1/2m_(alpha)v_(alpha)^(2)=k(2exxze)/(R)rArrR=(4kze^(2))/(m_(alpha)v_(alpha)^(2)`
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
`R=R_(0)(A)^(1//3)`
where `R_(0) = 1.2xx10^(-15)m`
A= atomic mass number
R=radius of nucleus
If `alpha-`particle with speed `v_(0)` is projected from infinity and it approaches upto `r_(0)` distance from the nuclei. Then the speed of `alpha-`particle which approaches `2r_(0)` distance from the nucleus is

Read the following passage carefully and answer the questions The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's alpha- scattering experiment. If an alpha- perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha- perticle which is reflected back or which is deflected by 180^(@) must have approach closest to the nucleus. It can be approximated that alpha- particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then: ("Total Energy")_("initial") = ("Total Enregy")_("final") (KE)_(i) +(PE)_(i)=(KE)_(f)+(PE)_(f) (PE)_(i) =0, "since"PE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back. 1/2m_(alpha)v_(alpha)^(2) + 0=0 + (kq_(1)q_(2))/(R) rArr1/2m_(alpha)v_(alpha)^(2)=k(2exxze)/(R)rArrR=(4kze^(2))/(m_(alpha)v_(alpha)^(2) Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as R=R_(0)(A)^(1//3) where R_(0) = 1.2xx10^(-15)m A= atomic mass number R=radius of nucleus If the diameter of two different nuclei are in the ratio 1:2 then their mass number are in the ratio:

Read the following passage carefully and answer the questions The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's alpha- scattering experiment. If an alpha- perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha- perticle which is reflected back or which is deflected by 180^(@) must have approach closest to the nucleus. It can be approximated that alpha- particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then: ("Total Energy")_("initial") = ("Total Enregy")_("final") (KE)_(i) +(PE)_(i)=(KE)_(f)+(PE)_(f) (PE)_(i) =0, "since"PE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back. 1/2m_(alpha)v_(alpha)^(2) + 0=0 + (kq_(1)q_(2))/(R) rArr1/2m_(alpha)v_(alpha)^(2)=k(2exxze)/(R)rArrR=(4kze^(2))/(m_(alpha)v_(alpha)^(2) Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as R=R_(0)(A)^(1//3) where R_(0) = 1.2xx10^(-15)m A= atomic mass number R=radius of nucleus Radius of a particular nucleus is calculated by the projection of alpha- particle from infinity at a particular speed. Let this radius be the true radius. If the radius calculation for the same nucleus is made by , alpha- particle with half of the earlier speed then the percentage error involved in the radius calculation is :

Rutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's alpha -scattering experiment. If an alpha -particle is projected from infinity with speed v towards the nucleus having Z protons, then the alpha -particle which is reflected back or which is deflected by 180^@ must have approached closest to the nucleus .It can be approximated that alpha particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then: (P.E.)_i= 0 , since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back. 1/2m_alpha v_alpha^2+0=0+(Kq_1q_2)/Rimplies 1/2m_alphav_alpha^2=K(2exxZe)/R implies R=(4KZe^2)/(m_alphav_alpha^2) Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it An alpha -particle with initial speed v_0 is projected from infinity and it approaches up to r_0 distance from a nuclie. Then, the initial speed of alpha -particle, which approaches upto 2r_0 distance from the nucleus is :

Rutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's alpha -scattering experiment. If an alpha -particle is projected from infinity with speed v towards the nucleus having Z protons, then the alpha -particle which is reflected back or which is deflected by 180^@ must have approached closest to the nucleus .It can be approximated that alpha particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then: (P.E.)_i= 0 , since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back. 1/2m_alpha v_alpha^2+0=0+(Kq_1q_2)/Rimplies 1/2m_alphav_alpha^2=K(2exxZe)/R implies R=(4KZe^2)/(m_alphav_alpha^2) Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it An alpha -particle with initial speed v_0 is projected from infinity and it approaches up to r_0 distance from a nuclie. Then, the initial speed of alpha -particle, which approaches upto 2r_0 distance from the nucleus is :

Rutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's alpha -scattering experiment. If an alpha -particle is projected from infinity with speed v towards the nucleus having Z protons, then the alpha -particle which is reflected back or which is deflected by 180^@ must have approached closest to the nucleus .It can be approximated that alpha particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then: (P.E.)_i= 0 , since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back. 1/2m_alpha v_alpha^2+0=0+(Kq_1q_2)/Rimplies 1/2m_alphav_alpha^2=K(2exxZe)/R implies R=(4KZe^2)/(m_alphav_alpha^2) Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it Radius of a particular nucleus is calculated by the projection of alpha -particle from infinity at a particular speed. Let this radius is the true radius . If the radius calculation for the same nucleus is made by another alpha -particle with half of the earlier speed, then the percentage error involved in the radius calculation is :

In Rutherford's scattering experiment of alpha -particles by metallic foils, with the increase of atomic number of nucleus, the scattering angle .

Rutherford's scattering experiment is related to the________of the nucleus.

Rutherford concluded from his alpha -ray scattering experiment that there exists a heavy and dense body at the centre of the nucleus .