Similar Questions
Explore conceptually related problems
Recommended Questions
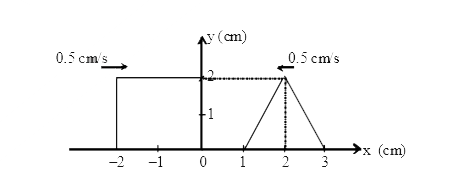
- Figure shows a rectangular pulse and a triangular pulse approaching ea...
Text Solution
|
- Two wave pulses travel in opposite directions on a string and approach...
Text Solution
|
- Figure shows a wave pulse at t=0. The pulse moves to the right with a ...
Text Solution
|
- If at t = 0, a travelling wave pulse in a string is described by the f...
Text Solution
|
- If at t = 0 , a travelling wave pulse on a string is described by the ...
Text Solution
|
- The figure shown at time t = 0 second, a rectangular and triangular pu...
Text Solution
|
- A hypothetical pulse is travelling along positive x direction on a tau...
Text Solution
|
- If wave y = A cos (omegat + kx) is moving along x-axis The shape of pu...
Text Solution
|
- Two pulses in a stretched string whose centres are initially 8 cm apar...
Text Solution
|