Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROMAGNETIC INDUCTION
KUMAR PRAKASHAN|Exercise Section B (Numerical) Numerical From Textual Exercise|17 VideosELECTROMAGNETIC INDUCTION
KUMAR PRAKASHAN|Exercise Section B (Numerical) Numerical From DARPAN Based on Textbook|10 VideosELECTROMAGNETIC INDUCTION
KUMAR PRAKASHAN|Exercise Section A HOTS|2 VideosELECTRIC CHARGES AND FIELDS
KUMAR PRAKASHAN|Exercise SECTION D MCQS ASKED IN COMPETITIVE EXAMES (MCQS AKSED IN BOARD EXAM AND GUJCET)|14 VideosELECTROMAGNETIC WAVES
KUMAR PRAKASHAN|Exercise BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C|5 Videos
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-ELECTROMAGNETIC INDUCTION-Section B (Numerical) Textual Illustrations
- Figure shows planar loops of different shapes moving out of or into a ...
Text Solution
|
- (a) A closed loop is held stationary in the magnetic field between the...
Text Solution
|
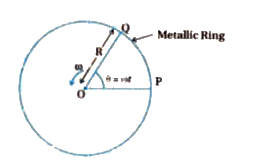
- A metallic rod of 1 m length is rotated with a frequency of 50 rev/s, ...
Text Solution
|
- A wheel with 10 metallic spokes each 0.5 m long is rotated with a spee...
Text Solution
|
- Refer to figure the arm PQ of the rectangular conductor is moved from ...
Text Solution
|
- Two concentric circular coils, one of small radius r1 and the other of...
Text Solution
|
- (a)Obtain the expression for the magnetic energy stored in a solenoid ...
Text Solution
|
- Kamla peddles a stationary bicycle. The pedals of the bicycle are atta...
Text Solution
|
- A square loop of side 10 cm and resistance 0.5 Omega is placed vertica...
Text Solution
|
- A square loop of side 10 cm and resistance 0.5 Omega is placed vertica...
Text Solution
|
- A circular coil of radius 10 cm, 500 turns and resistance 2Omega is pl...
Text Solution
|
- A circular coil of radius 20 cm, 500 turns and resistance 4Omega is p...
Text Solution
|
- A wheel of radius r having conducting rim and n no. of conducting spok...
Text Solution
|
- One metallic ring of radius 2 m has a conducting rod connected between...
Text Solution
|
- One metallic ring of radius 1 m has a conducting rod connected between...
Text Solution
|
- A wheel with 100 metallic spokes each 1 m long is rotated with a speed...
Text Solution
|
- A wheel with 10 metallic spokes each 1 m long is rotated with a speed ...
Text Solution
|
- One U shaped conducting frame is placed in a plane perpendicular to un...
Text Solution
|
- As shown in the figure, a conducting rod of length I, mass m and resis...
Text Solution
|
- One extremely small and another extremely big square frames are coplan...
Text Solution
|