Similar Questions
Explore conceptually related problems
Recommended Questions
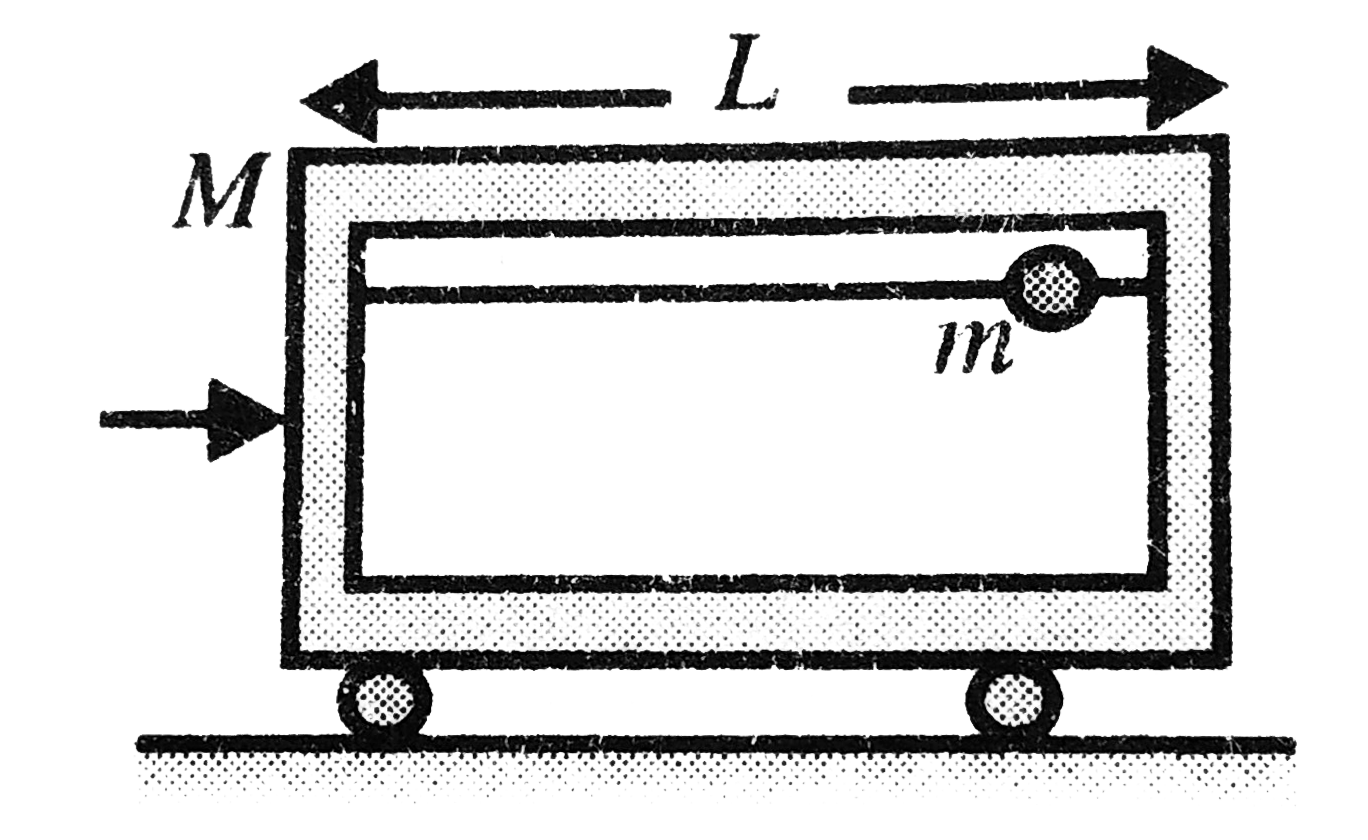
- A horizontal frictionless rod is threaded through a bead of mass m. Th...
Text Solution
|
- A horizontal frictionless rod is threaded through a bead of mass m . T...
Text Solution
|
- A horizontal frictionless rod is threaded through a bead of mass m . T...
Text Solution
|
- A horizontal frictionless rod is threaded through a bead of mass m . T...
Text Solution
|
- Two beads of mass 2m and m , connected by a rod of length l and of neg...
Text Solution
|
- A bead can slide on asmooth straight wire and a particle of mass m att...
Text Solution
|
- A bead is connected with a fixed disc of radius R by an inextensible m...
Text Solution
|
- A bead moves along a straight horizontal wire of length L, starting fr...
Text Solution
|
- A rigid mass less rod of length L is rotating in a vertical plane abou...
Text Solution
|