Similar Questions
Explore conceptually related problems
Recommended Questions
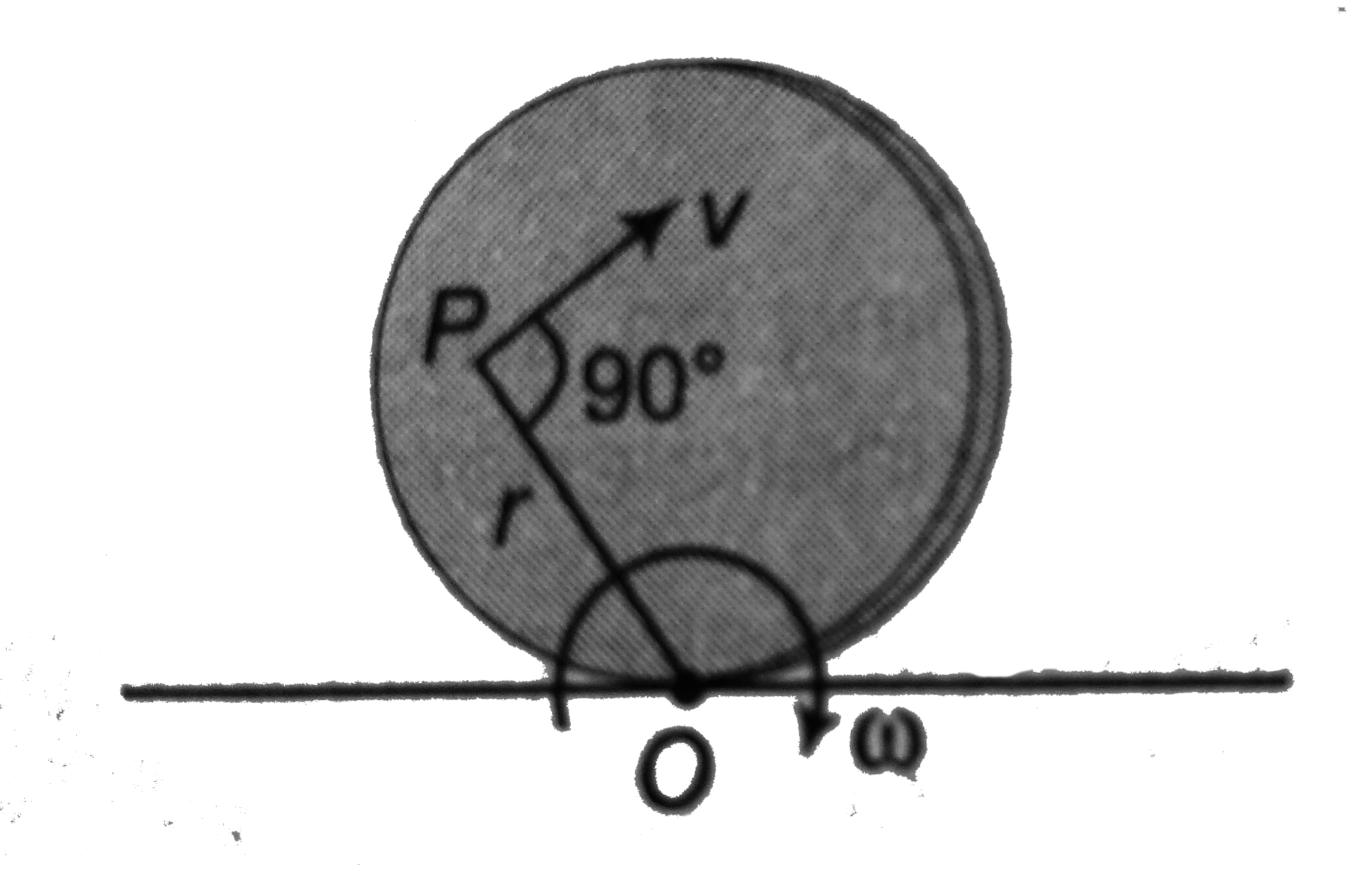
- Using the concept of instantaneous axis of rotation. Find speed of par...
Text Solution
|
- Using the concept of instantaneous axis of rotation. Find speed of par...
Text Solution
|
- A disc is rolling without slipping with linear velocity v as shown in ...
Text Solution
|
- Assertion: A ball is released on a rough ground in the condition shown...
Text Solution
|
- A liquid of density 'rho' is rotated with an angular speed 'omega' as ...
Text Solution
|
- Shown in the figure is rod which moves with v=2ms^(-1) and rotates wit...
Text Solution
|
- A disc is rolling on a rough horizontal surface. The instantaneous spe...
Text Solution
|
- What is the condition for pure rolling ?
Text Solution
|
- Rotational Motion - Instantaneous Axis Of Rotation
Text Solution
|