Text Solution
Verified by Experts
Topper's Solved these Questions
THERMODYANMICS
KUMAR PRAKASHAN|Exercise Section-A (Try Your self )|90 VideosTHERMODYANMICS
KUMAR PRAKASHAN|Exercise Section-B Numericals (Numerical From Textual Exercise)|10 VideosTHERMAL PROPERTIES OF MATTER
KUMAR PRAKASHAN|Exercise Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks|1 VideosUNITS AND MEASUREMENT
KUMAR PRAKASHAN|Exercise Section -F (Questions from Module )|20 Videos
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-THERMODYANMICS -Question Paper
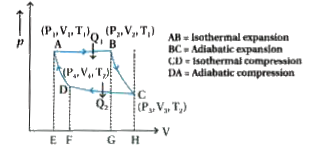
- Show four steps of carnot engine in P-V graph write the equation of ea...
Text Solution
|
- Why is a steam burn more damaging than a burn with boiling water of th...
Text Solution
|
- What is coefficient of performance of a refrigerator ?
Text Solution
|
- With whom thermodynamics state be decided ?
Text Solution
|
- What is latent heat of vaporization ?
Text Solution
|
- On what the values of heat (Q) and work (W) depends in thermodynamics ...
Text Solution
|
- Give the relationship between pressure and volume in an adiabatic proc...
Text Solution
|
- Discuss when can you say that the system is in thermal equilibrium and...
Text Solution
|
- Obtain an expression of work for the compression of gas at constant te...
Text Solution
|
- What amount of heat must be supplied to 2.0 xx 10^(-2) Kg of nitrogen ...
Text Solution
|
- A cylinder with a movable piston contains 3 moles of hydrogen at stand...
Text Solution
|
- In changing the state of a gas adiabatically from an equilibrium state...
Text Solution
|