Text Solution
Verified by Experts
Topper's Solved these Questions
THERMODYANMICS
KUMAR PRAKASHAN|Exercise Section-E MCQs|42 VideosTHERMODYANMICS
KUMAR PRAKASHAN|Exercise Section-F Questions from Module|20 VideosTHERMODYANMICS
KUMAR PRAKASHAN|Exercise Section-D Ncert Exemplar Solution (Short Answer )|6 VideosTHERMAL PROPERTIES OF MATTER
KUMAR PRAKASHAN|Exercise Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks|1 VideosUNITS AND MEASUREMENT
KUMAR PRAKASHAN|Exercise Section -F (Questions from Module )|20 Videos
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-THERMODYANMICS -Section-D Ncert Exemplar Solution (Long Answer )
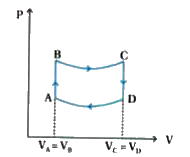
- Consider a P-V diagram in which the path followed by one mole of perfe...
Text Solution
|
- A cycle followed by an engine (made of one mole of perfect gas in a cy...
Text Solution
|
- A cycle followed by an engine (made of one mole of an ideal gas in a c...
Text Solution
|
- Consider that an ideal gas (n moles) is expanding in a process given b...
Text Solution
|
- Consider one mole of perfect gas in a cylinder of unit cross section w...
Text Solution
|