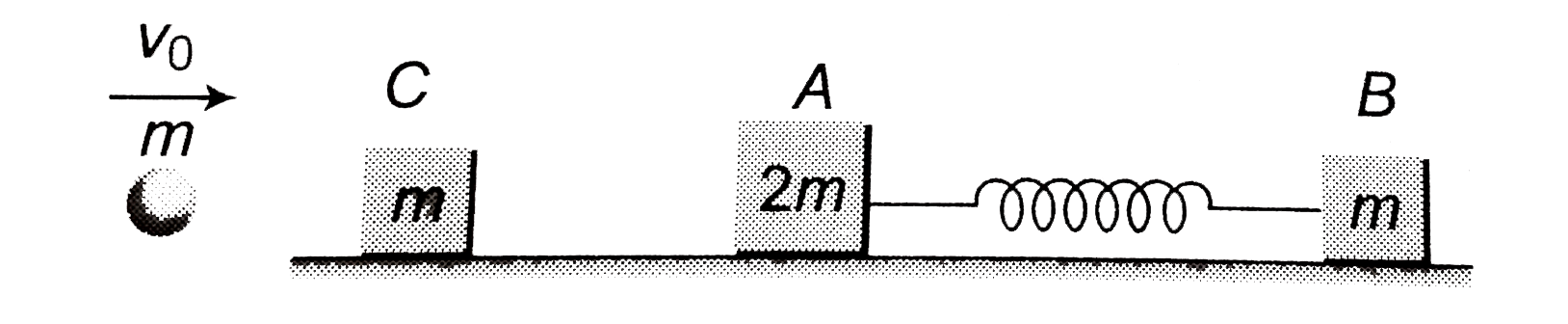Similar Questions
Explore conceptually related problems
Recommended Questions
- The ball sticks to block C, then block Ccollides elastically , head - ...
Text Solution
|
- The block of mass M moving on the frictionless horizontal surface col...
Text Solution
|
- A block of mass m is suddenly released from the top of a spring of sti...
Text Solution
|
- A block of mass m moving at a speed v0 compresses a spring of spring c...
Text Solution
|
- The ball strikes the block and sticks to it. Find the maximum compress...
Text Solution
|
- If blocks collide elastically head - on , the ratio of maximum compres...
Text Solution
|
- The ball sticks to block C, then block Ccollides elastically , head - ...
Text Solution
|
- Two blocks A and B of mass 2 m and m respectively are connected to a m...
Text Solution
|
- Block C of mass M is moving with velocity V(0) and collides elasticall...
Text Solution
|