Similar Questions
Explore conceptually related problems
Recommended Questions
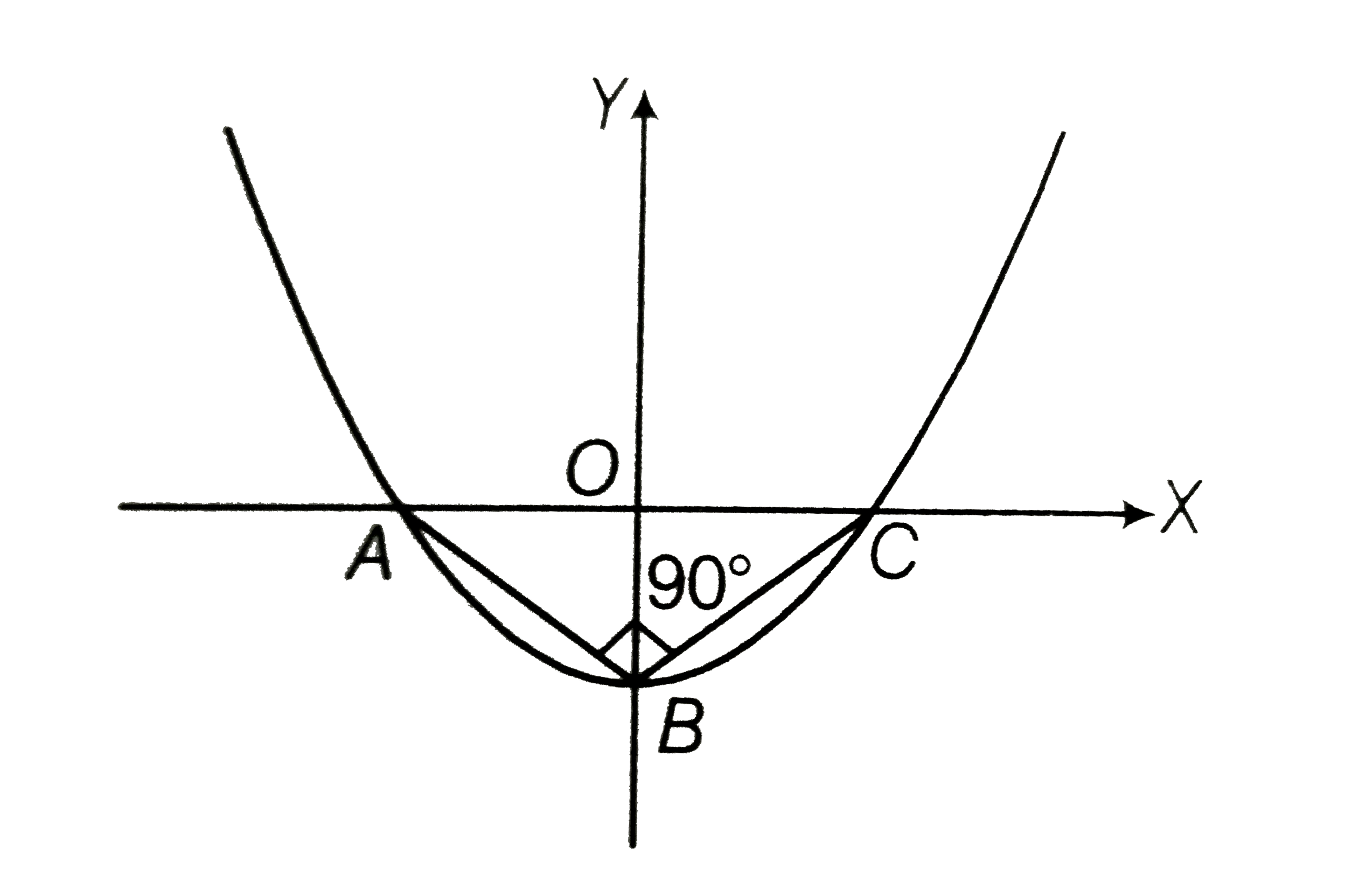
- In the given figue vertices of DeltaABC lie on y=f(x)=ax^(2)+bx+c. The...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- The inequation represented by the graph given below is : <img src="htt...
Text Solution
|
- The inequation that best describes the graph given below is <img src=...
Text Solution
|
- In the given figue vertices of DeltaABC lie on y=f(x)=ax^(2)+bx+c. The...
Text Solution
|
- In the given figue vertices of DeltaABC lie on y=f(x)=ax^(2)+bx+c. The...
Text Solution
|
- In the given figue vertices of DeltaABC lie on y=f(x)=ax^(2)+bx+c. The...
Text Solution
|
- दिये गये चित्र में DeltaABC के शीर्ष y=f(x)=ax^(2)+bx+c पर स्थित है De...
Text Solution
|
- दिये गये चित्र में DeltaABC के शीर्ष y=f(x)=ax^(2)+bx+c पर स्थित है De...
Text Solution
|