Similar Questions
Explore conceptually related problems
Recommended Questions
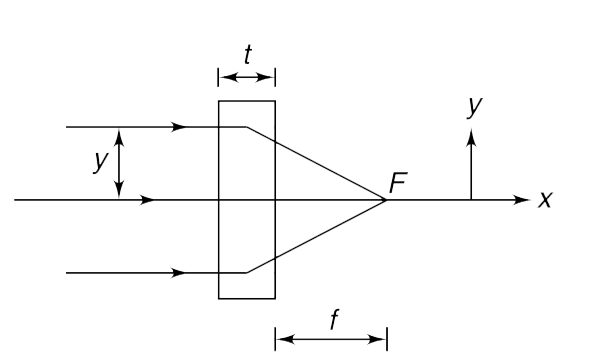
- A parallel beam of light travelling in x direction is incident on a gl...
Text Solution
|
- An intially parallel cyclindrical beam travels in a medium of refracti...
Text Solution
|
- An intially parallel cyclindrical beam travels in a medium of refracti...
Text Solution
|
- An intially parallel cyclindrical beam travels in a medium of refracti...
Text Solution
|
- A parallel beam of light travelling in x direction is incident on a gl...
Text Solution
|
- The refractive index of a medium changes asmu=mu(0)[1-(x^(2)+y^(2))/(d...
Text Solution
|
- A light ray travelling in a medium of refractive index mu(1) is incide...
Text Solution
|
- A convex lens of refractive index mu(1) is kept in a medium of refract...
Text Solution
|
- A concave lens of refractive index mu(1) is kept in a medium of refrac...
Text Solution
|