Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTRIC CHARGES AND FIELDS
KUMAR PRAKASHAN|Exercise SECTION A QUESTIONS- ANSWERS (TRY YOURSELF )|73 VideosELECTRIC CHARGES AND FIELDS
KUMAR PRAKASHAN|Exercise SECTION B NUMERICALS (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)|24 VideosELECTRIC CHARGES AND FIELDS
KUMAR PRAKASHAN|Exercise SECTION A QUESTIONS- ANSWERS (FIELD DUE TO AN UNIFORMLY CHARGED INFINITE PLANE SHEET)|1 VideosDUAL NATURE OF RADIATION AND MATTER
KUMAR PRAKASHAN|Exercise Section-D (MCQs asked in GUJCET/Board Exam)|1 VideosELECTROMAGNETIC INDUCTION
KUMAR PRAKASHAN|Exercise Section D MCQs (MCQs asked in Competitive Exams )|38 Videos
Similar Questions
Explore conceptually related problems
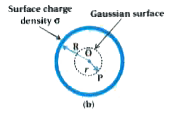
KUMAR PRAKASHAN-ELECTRIC CHARGES AND FIELDS -SECTION A QUESTIONS- ANSWERS (FIELD DUE TO A UNIFORMLY CHARGED THIN SPHERICAL SHELL)
- Obtain the expression of electric field by thir spherical shell with u...
Text Solution
|
- Obtain the expression of electric field by thin spherical shell with u...
Text Solution
|
- Explain by graph how the electric field by thin spherical shell depend...
Text Solution
|
- Obtain the expression of electric field by thir spherical shell with u...
Text Solution
|
- Obtain Gauss's law from Coulomb's law.
Text Solution
|
- Obtain Coulomb's law from Gauss's law.
Text Solution
|