Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROMAGNETIC WAVES
KUMAR PRAKASHAN|Exercise SECTION D MULTIPLE CHOICE QUESTIONS (MCQs)|76 VideosELECTROMAGNETIC WAVES
KUMAR PRAKASHAN|Exercise SECTION D MULTIPLE CHOICE QUESTIONS (MCQs) MCQs asked in Competitive Exams|23 VideosELECTROMAGNETIC WAVES
KUMAR PRAKASHAN|Exercise SECTION C NCERT EXEMPLAR SOLUTION (Short Answer Type Questions)|9 VideosELECTROMAGNETIC INDUCTION
KUMAR PRAKASHAN|Exercise Section D MCQs (MCQs asked in Competitive Exams )|38 VideosELECTROSTATIC POTENTIAL AND CAPACITANCE
KUMAR PRAKASHAN|Exercise Section D ( MCQs asked in Cometitive Exams )|39 Videos
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-ELECTROMAGNETIC WAVES-SECTION C NCERT EXEMPLAR SOLUTION (Long Answer Type Questions)
- An infinitely long thin wire carrying a uniform linear static charge d...
Text Solution
|
- Sea water at frequency v=4xx10^(8) Hz has permittivity in ~~ 80 in(0),...
Text Solution
|
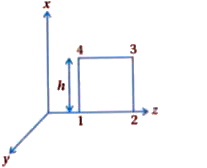
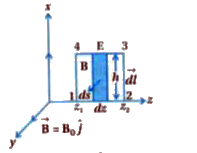
- A long straight cable of length l is placed symmetrically along z - ax...
Text Solution
|
- A long straight cable of length l is placed symmetrically along z - ax...
Text Solution
|
- A long straight cable of length l is placed symmetrically along z - ax...
Text Solution
|
- A plane EM wave travelling in vacuum along z - direction is given by v...
Text Solution
|
- A plane EM wave travelling in vacuum along z - direction is given by v...
Text Solution
|
- A plane EM wave travelling in vacuum along z - direction is given by v...
Text Solution
|
- A plane EM wave travelling in vacuum along z - direction is given by v...
Text Solution
|
- A plane EM wave travelling along z - direction is desctribed vec(E )=E...
Text Solution
|
- A plane EM wave travelling along z - direction is desctribed vec(E )=E...
Text Solution
|